Motion in Two Dimensions with Constant Acceleration

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
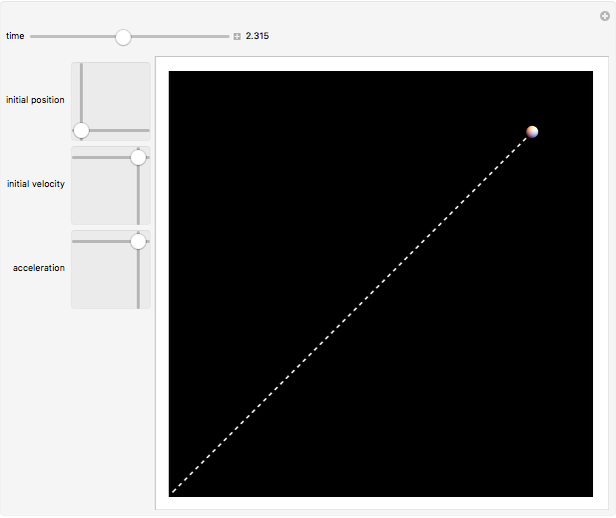
A particle starting at position  with initial velocity
with initial velocity  subjected to a constant acceleration
subjected to a constant acceleration  follows a trajectory given by
follows a trajectory given by  . For one-dimensional motion, say in the
. For one-dimensional motion, say in the  direction, this reduces to
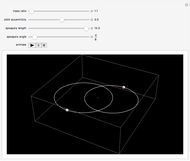
direction, this reduces to  . A projectile fired upward at an angle describes a parabolic trajectory when subject to the downward acceleration of gravity. The path of the particle up to the time
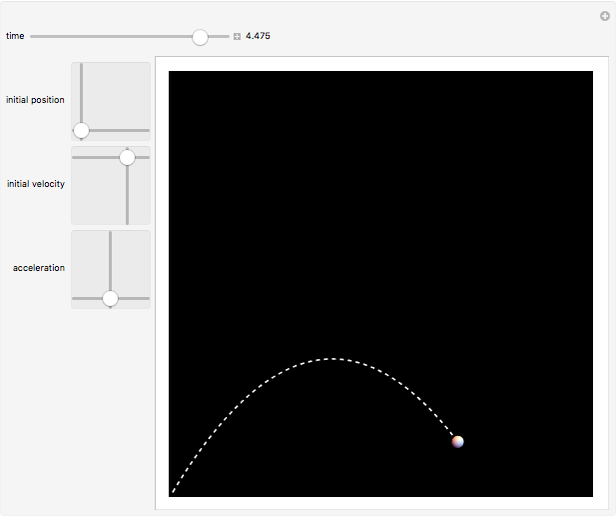
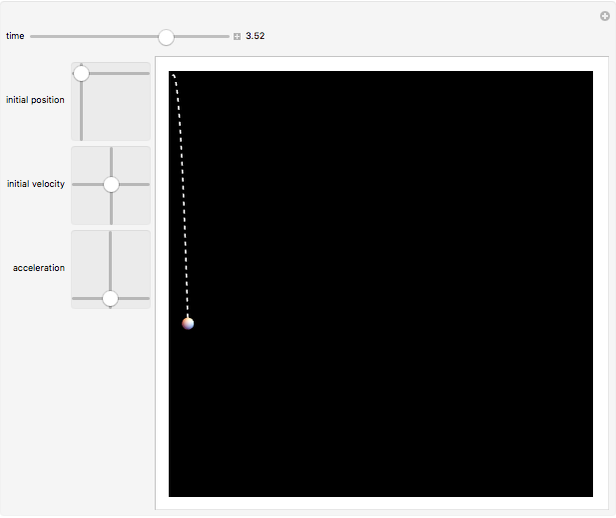
. A projectile fired upward at an angle describes a parabolic trajectory when subject to the downward acceleration of gravity. The path of the particle up to the time  is shown by a dotted curve.
is shown by a dotted curve.
Contributed by: S. M. Blinder (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
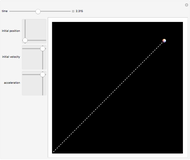
Snapshot 1: linear motion when the velocity and acceleration are in the same direction
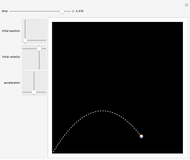
Snapshot 2: parabolic trajectory of a missile
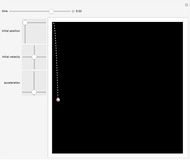
Snapshot 3: a weight dropped, possibly off the Tower of Pisa, with a slight forward push
You can animate these simulations with the animation button on the time slider. Use the slow motion option.
Reference: E. Kasner, "The Trajectories of Dynamics," Transactions of the American Mathematical Society, 7(3) 1906 pp. 401–424.
Permanent Citation
"Motion in Two Dimensions with Constant Acceleration"
http://demonstrations.wolfram.com/MotionInTwoDimensionsWithConstantAcceleration/
Wolfram Demonstrations Project
Published: March 7 2011