Wolfram Demonstrations Project

12,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

Motion of Quadruple Pendulum

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

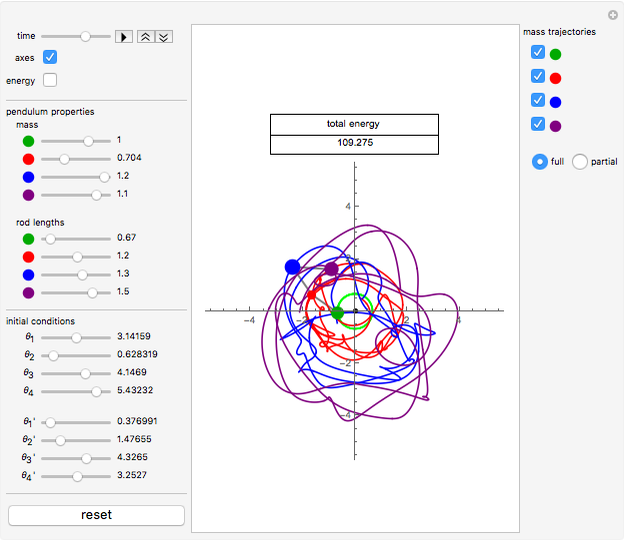
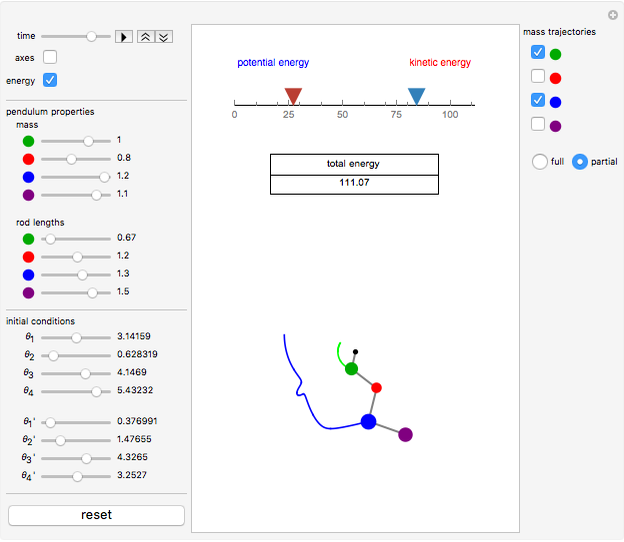
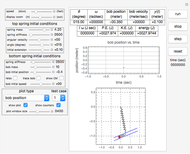
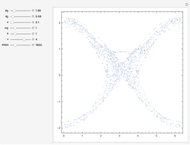
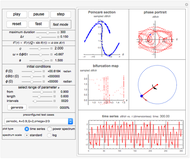
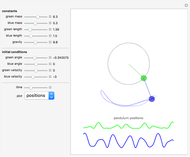
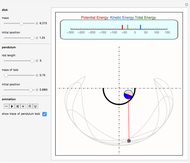
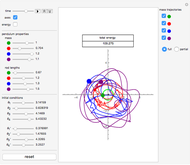
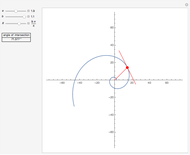
This Demonstration shows the motion of a quadruple pendulum, consisting of four point masses connected by massless rods. In common with the double and triple pendulum, the quadruple pendulum can exhibit chaotic behavior. After you change a control, click the "reset" button to see the effect.

[more]

The equations of motion for each mass in the quadruple pendulum system are second-order differential equations derived from the Euler–Lagrange equation. These second-order differential equations are solved via Mathematica's NDSolve function.

In this system, the potential energy of each of the masses increases with its height. The total potential and kinetic energies, along with the conserved total energy, are shown in the graphic.

[less]

Contributed by: Vighnesh Souda (March 2015)
Enhanced by: Erik Mahieu
Open content licensed under CC BY-NC-SA

Snapshots

Details

Following are the steps for finding the equations of motion for each mass in the quadruple pendulum:

1. Find the equations for both kinetic energy and potential energy.

2. From these equations, calculate the Lagrangian by subtracting potential energy from kinetic energy.

3. The partial derivative of the Lagrangian with respect to the derivative of each angle is calculated (call this expression 1).

4. Calculate the derivative of expression 1 with respect to time (call this expression 2).

5. Calculate the partial derivative of the Lagrangian with respect to each angle (call this expression 3).

6. Set expressions 2 and 3 equal to form the Euler–Lagrange differential equation.

There are four Euler–Lagrange differential equations, all of which are second order. Each of these four equations correlates to the angle of the corresponding mass in the quadruple pendulum.

Reference

[1] W. S. Harvie. "AP Physics C Notes." (Mar 26, 2015) teachers.sduhsd.net/tpscience/physics/notes/AP%20 Physics %20 C %20 Notes %20-%20 Mechanics/166%20-%20209 E %20 Harmonic %20 Oscillations.pdf.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send