Details

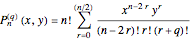
are known as hybrid polynomials [1], since they share evident analogies with Laguerre and Hermite polynomials.

They are indeed generated by the function

,

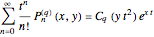where the Tricomi–Bessel function is defined by the series

,

which, in the present context, is viewed as a pseudo-exponential function. Using the same point of view developed in [2, 3], from the operational point of view, they are generated from the ordinary monomials according to the relation

,

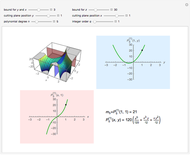
where 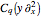is a pseudo-exponential diffusion operator. The geometrical content of the last equation can be understood according to the strategy developed in [2, 3] and is shown in -- space in Snapshot 1. According to the figures, the pseudo-exponential operator transforms an ordinary monomial 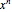into a special polynomial of the hybrid type. The monomial-polynomial evolution is shown by moving the cutting plane orthogonal to the  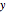axis. On each of the cutting planes, different families of polynomials are defined. For example, for a given 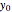, are polynomials of Lengendre type according to [1]. It is worth stressing that the polynomials exhibit zeros (thus providing orthogonal families) only for negative values of 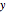, as in Snapshot 2.

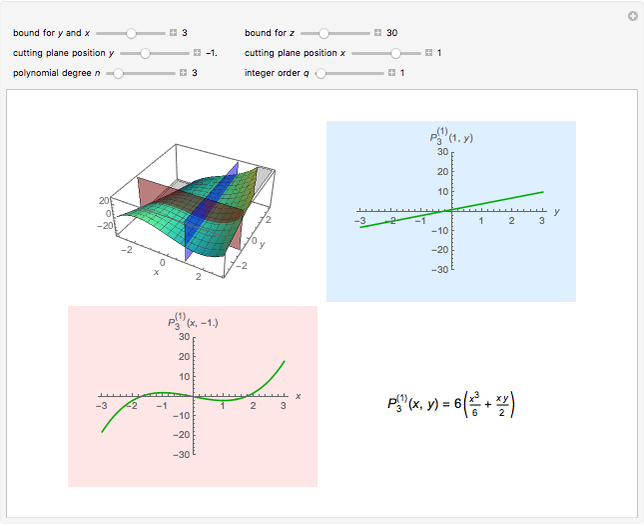
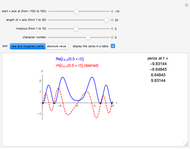
The case is shown in Snapshot 2, where we have reported the geometrical interpretation [4] in the --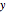 space of the hybrid polynomials 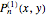. It is worth noting that the Motzkin numbers [5] emerge as specific values of the polynomials 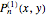calculated for 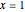, , 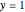namely

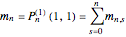
where

.

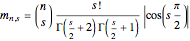Thus the whole sequence yielding the Motzkin numbers, labeled by the integer , is represented by

.

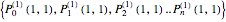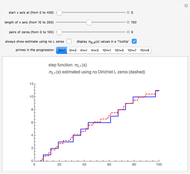
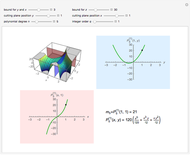
In [6–8] we have provided the geometrical interpretation of Padovan and Perrin numbers by means of the geometrical view of two-variable Legendre polynomials [9], while in this Demonstration we show that the Motzkin numbers correspond to the points (shown as black dots in Snapshot 2 in the graph for and 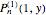) of the intersection of the two cutting planes with the surface 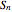corresponding to the polynomial 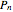as specified below

.

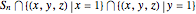This means that the representation of Motzkin numbers on the figures can be seen by moving the cutting planes to 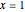and 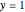, while keeping the order . The numbers correspond to the ordinates (that is to the values of 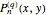read on the vertical axis, when ) and are represented by a black dot on the blue and pink planes. The full sequence of Motzkin numbers can be explored by leaving and then moving the slider for : the black dots will move (because the 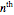number is generally different from the ) while remaining on the curves (which will change, instead). Also note that the two black dots on the blue and pink planes are for the same number (the same value of , actually), because two points of view (or projections) are reported.

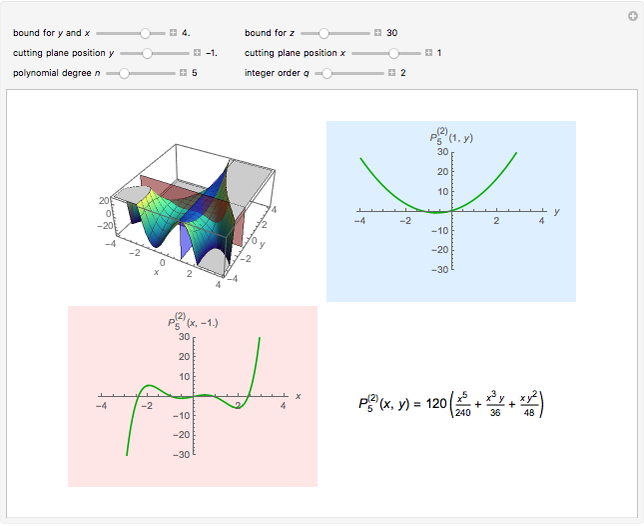
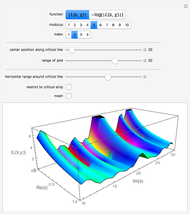
Snapshot 3, instead, shows a case for 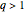, which extends the definition of Motzkin numbers to higher orders, but they will be presented in a forthcoming Demonstration.

References

[1] G. Dattoli, S. Lorenzutta, P. E. Ricci and C. Cesarano, "On a Family of Hybrid Polynomials," Integral Transforms and Special Functions, 15(6), 2004 pp. 485–490. doi:10.1080/10652460412331270634.

[2] M. Artioli and G. Dattoli. "Geometric Properties of Generalized Hermite Polynomials" from the Wolfram Demonstrations Project—A Wolfram Web Resource. demonstrations.wolfram.com/GeometricPropertiesOfGeneralizedHermitePolynomials.

[3] M. Artioli and G. Dattoli. "Geometry of Two-Variable Laguerre Polynomials" from the Wolfram Demonstrations Project—A Wolfram Web Resource. demonstrations.wolfram.com/GeometryOfTwoVariableLaguerrePolynomials.

[4] E. W. Weisstein. "Motzkin Number" from MathWorld—A Wolfram Web Resource. mathworld.wolfram.com/MotzkinNumber.html (Wolfram MathWorld).

[5] P. Blasiak, G. Dattoli, A. Horzela, K. A. Penson and K. Zhukovsky, "Motzkin Numbers, Central Trinomial Coefficients and Hybrid Polynomials." Journal of Integer Sequences, 11, 2008 Article 08.1.1. cs.uwaterloo.ca/journals/JIS/VOL11/Penson/penson131.pdf.

[6] M. Artioli and G. Dattoli. "Geometric Interpretation of Perrin and Padovan Numbers" from the Wolfram Demonstrations Project—A Wolfram Web Resource. demonstrations.wolfram.com/GeometricInterpretationOfPerrinAndPadovanNumbers.

[7] E. W. Weisstein. "Perrin Sequence" from MathWorld—A Wolfram Web Resource. mathworld.wolfram.com/PerrinSequence.html (Wolfram MathWorld).

[8] E. W. Weisstein. "Padovan Sequence" from MathWorld—A Wolfram Web Resource. mathworld.wolfram.com/PadovanSequence.html (Wolfram MathWorld).

[9] M. Artioli and G. Dattoli, "Geometry of Two-Variable Legendre Polynomials" from the Wolfram Demonstrations Project—A Wolfram Web Resource. demonstrations.wolfram.com/GeometryOfTwoVariableLegendrePolynomials.