Wolfram Demonstrations Project

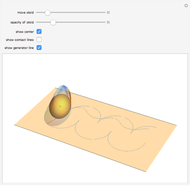
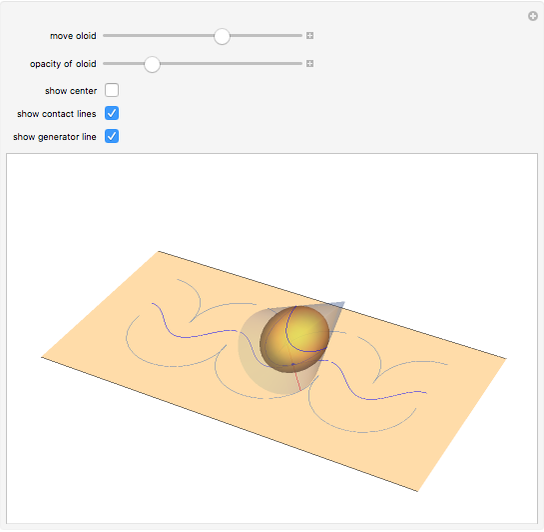
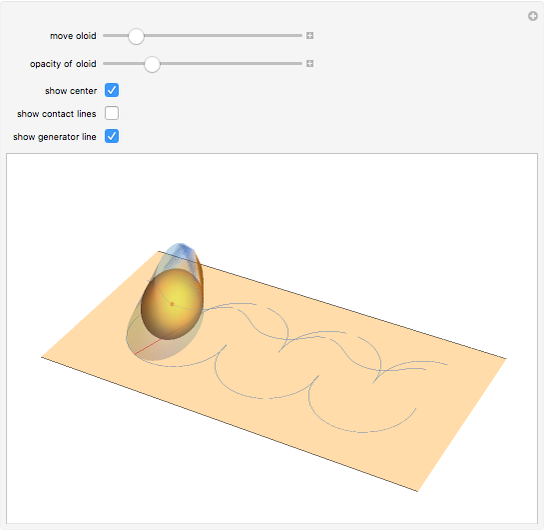
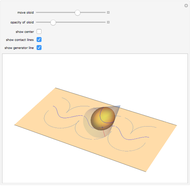
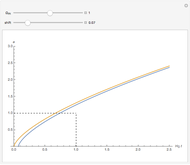
You see the wobbling motion of an oloid on a plane while making one-and-a-half turns, and can observe how this motion can be described by the locus of the brims in the plane. The plane is tangent to the surface of the oloid, and the set of all tangent planes can be used to define an inscribed body. When you reduce the opacity of the oloid, this inscribed body, an ellipsoid, becomes visible. The locus of the center of gravity of the oloid, the trajectories of the contact point between the ellipsoid and the plane, and the generator line can be shown.

Contributed by: Hans-Joachim Domke

Rotate and Zoom in 3D
Slider Zoom
Gamepad Controls
Automatic Animation

The oloid is also called a two-circle roller (TCR) because its parametrical description is based on two points

and

on two unit circles

and

that are perpendicular to each other and mutually contain the center of the other.

and

are conjugated by the point

so that

and

are tangents to the respective circle. The line

is called the generator line.

is symmetrical to

with respect to the

axis, so

is also a generator, which is chosen here because when TCR is set on a plane,

and

get in contact with the plane and so are all points on

With the generator line, the oloid can be described parametrically so it is necessary to know the position of

at any time. In the original coordinate system with origin at the center of the oloid, the location of

is determined by the angle

; to describe the moving oloid, a new coordinate system in the plane is needed in which

must also depend on

Let

coincide with the point

in the plane when

, with

as the origin of the new coordinate system. On the way to the position shown, the point

leaves a trace on the plane, the blue arc. It has the same length as the arc on

and because this depends on

, the arc length of the blue trajectory can be expressed as a function of

. The arc length of the trajectory can be calculated by integrating over the curvature

twice.

We have that

and there are two more integrals to get the parametrization of the arc-length. In [1] an exact solution is given and in [2] the integrals are solved numerically, but this slows the process of calculation dramatically so it is not acceptable for interactivity. The author converted the integrands of some of the integrals into power series to get an approximate solution to get the vector equation for the coordinate transformation, but this was not possible for all of the needed functions, so some of the solutions in [1] are used also. For a more detailed discussion of the mathematics involved, you may refer to the excellent articles [1] and [2].