Wolfram Demonstrations Project

12,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

Multiple-Link Functions

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

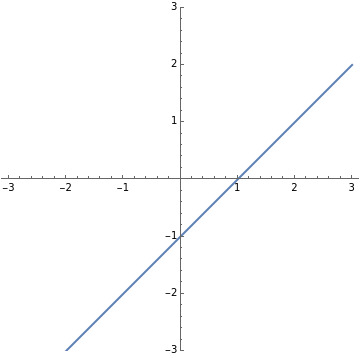
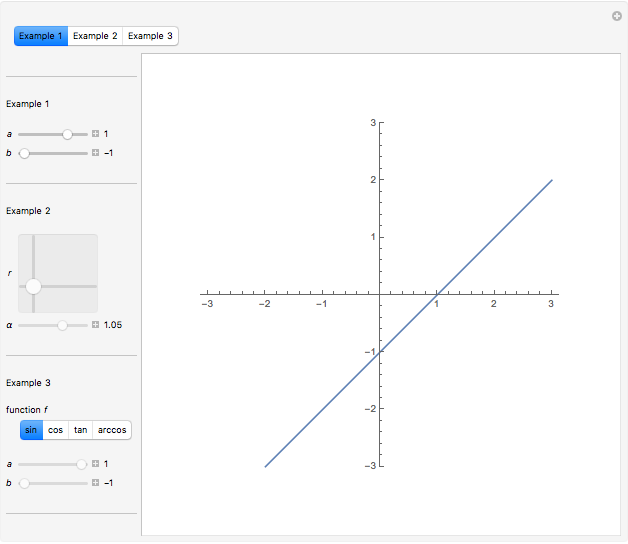
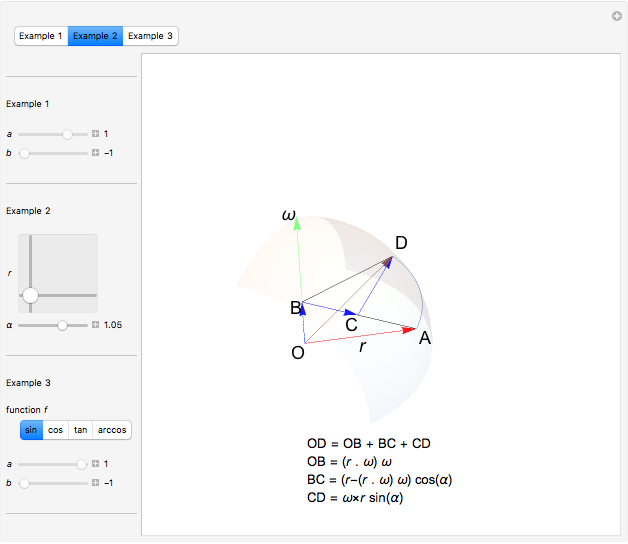
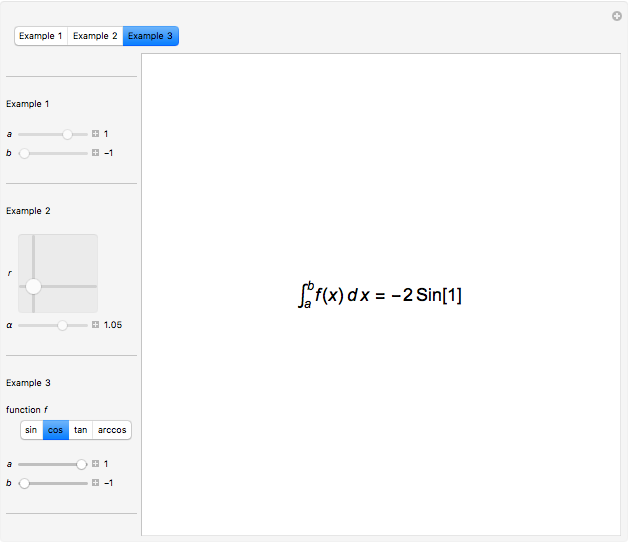
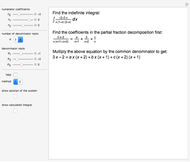
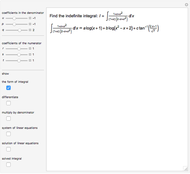
Multiple-link functions are functions that have arguments grouped in more than one pair of brackets. They appear in expressions of the type . Definitions of multiple-link functions enable the classification of arguments as either parameters or variables.

[more]

Example 1. The identity

defines a double-link function, where is a two-parameter family of linear functions.

Example 2. A formula for rotating the vector around the axis given by the unit vector through the angle is , involving dot and cross products of vectors.

Example 3. The identity

defines the definite integral of a function from to which avoids using the bound (or dummy) variable .

[less]

Contributed by: Izidor Hafner (May 2017)
Open content licensed under CC BY-NC-SA

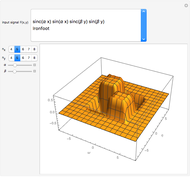
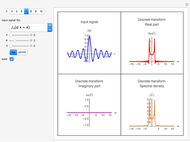
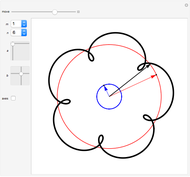
Snapshots

Details

Mathematica has recently introduced the operator-form functions SortBy[f], MaximalBy[f], TakeLargestBy[f,n] and so on.

References

[1] S. Leśniewski, S. Leśniewski's Lecture Notes in Logic (J. Srzednicki and Z. Stachniak, eds.), Boston: Kluwer Academic, 1988 p. 31.

[2] S. Leśniewski, Stanisław Leśniewski, Collected Works (S. J. Surma, J. T. Srzednicki and D. I. Barnett, eds.), Boston: Kluwer Academic, 1992 p. 475

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send