Multipole Expansions of Electric Fields

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
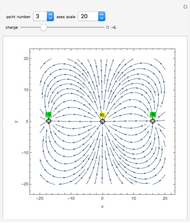
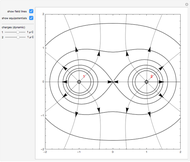
In classical electromagnetic theory, the potential of a reasonably localized charge distribution can be represented by a multipole expansion, which is based on a sum of terms of the form 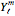 . The contributions from
. The contributions from  represent monopole, dipole, quadrupole and octupole sources, respectively, and sums of these can generate any realistic potential. The gradient of the potential gives the electric field. Gauss's law then equates the flux of the electric field through a Gaussian surface to the source density within the boundary of that surface. Though Gauss's law can facilitate the expression of the electric field of a point charge, expansion of the electric field created by a configuration of point charges requires a sum including higher-order multipole functions. Dipoles, quadrupoles and octupoles all have a unique angular distribution of flux, all of which integrate to zero. Each of these distributions represents a solution of Poisson's equation. The monopole potential (as from a point charge) is spherically symmetrical, varying as
represent monopole, dipole, quadrupole and octupole sources, respectively, and sums of these can generate any realistic potential. The gradient of the potential gives the electric field. Gauss's law then equates the flux of the electric field through a Gaussian surface to the source density within the boundary of that surface. Though Gauss's law can facilitate the expression of the electric field of a point charge, expansion of the electric field created by a configuration of point charges requires a sum including higher-order multipole functions. Dipoles, quadrupoles and octupoles all have a unique angular distribution of flux, all of which integrate to zero. Each of these distributions represents a solution of Poisson's equation. The monopole potential (as from a point charge) is spherically symmetrical, varying as  .
.
Contributed by: Brad Klee (May 2017)
Open content licensed under CC BY-NC-SA
Details
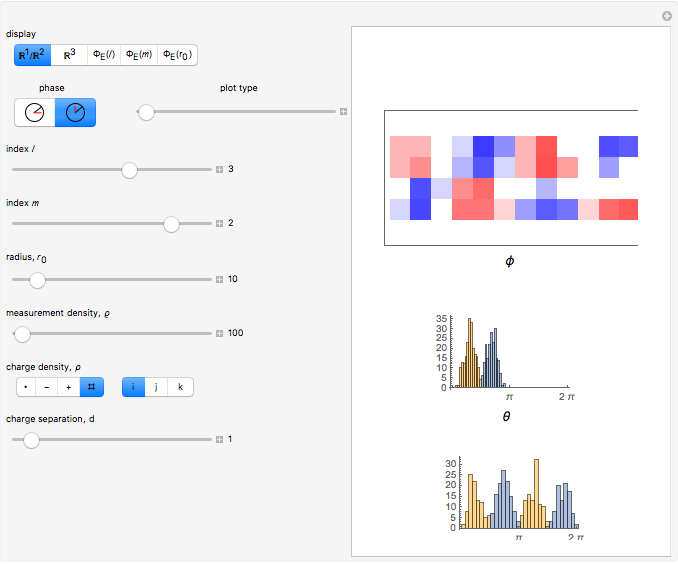
Exact forms for electric potentials can be found by integrating over the charge distribution of the source. A very useful representation is an expansion of the potential, expressed in terms of spherical harmonics, specifically of the form 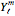 . Each of the monopole, dipole, quadrupole and octupole charge densities belongs to a
. Each of the monopole, dipole, quadrupole and octupole charge densities belongs to a  -dimensional representation of the 3-dimensional rotational group, with their characteristic symmetries. As an approximation to the exact solutions, a multipole expansion can be computed using numerical integration.
-dimensional representation of the 3-dimensional rotational group, with their characteristic symmetries. As an approximation to the exact solutions, a multipole expansion can be computed using numerical integration.
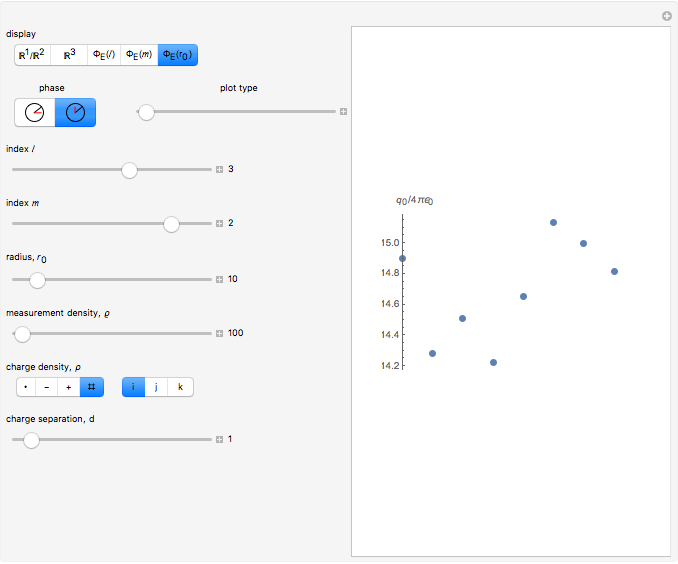
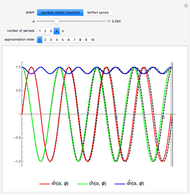
This Demonstration computes an electric flux through the surface of a sphere centered at the origin, multiplying a sample density constant by a sum of radial components of the electric field (multiplied by 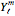 or
or  ) over a subset of all vectors with norm equal to
) over a subset of all vectors with norm equal to  , the radius of the surface of integration. When the subset of vectors is chosen from a distribution such that the sample can be described by one density as a function of solid angle, the computed quantity can equal the electric flux in Gauss's law. However, the uniform density in this Demonstration is chosen according to the isotropic spherical harmonic
, the radius of the surface of integration. When the subset of vectors is chosen from a distribution such that the sample can be described by one density as a function of solid angle, the computed quantity can equal the electric flux in Gauss's law. However, the uniform density in this Demonstration is chosen according to the isotropic spherical harmonic 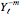 , leading to a computed value of approximately
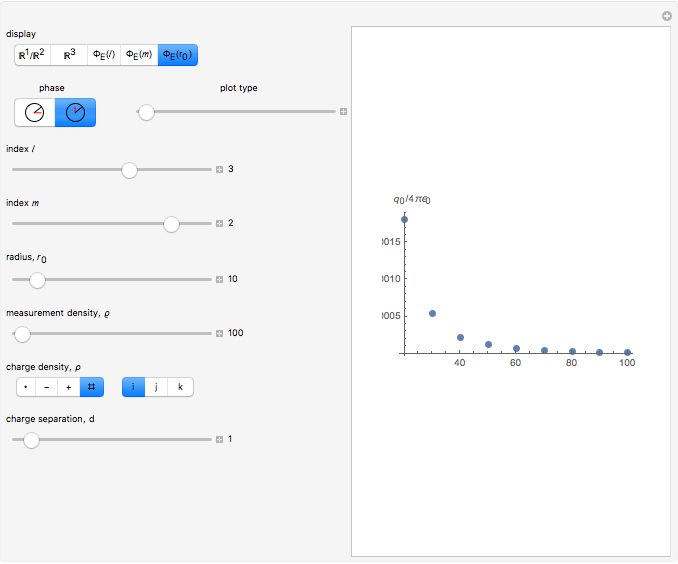
, leading to a computed value of approximately  for a point charge. Using this quantity as a coefficient for
for a point charge. Using this quantity as a coefficient for 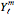 gives an expansion for the monopole electric field:
gives an expansion for the monopole electric field: 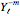 in units of
in units of 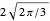 . Likewise, expansion coefficients for the radial component of electric fields, corresponding to higher-order multipole charge densities, can be computed by summing over a subset of vectors related to the spherical harmonics,
. Likewise, expansion coefficients for the radial component of electric fields, corresponding to higher-order multipole charge densities, can be computed by summing over a subset of vectors related to the spherical harmonics,  .
.
When an expansion includes a term 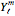 with
with  , it will also include
, it will also include  because the real (or imaginary) part of
because the real (or imaginary) part of 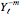 can be expressed as a multiple of the real (or imaginary) part of
can be expressed as a multiple of the real (or imaginary) part of  . Therefore, coefficients for the
. Therefore, coefficients for the 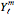 and
and 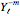 have been divided by two so that the expansion does not duplicate the contributions to the radial component of the electric field. For example, in this Demonstration, the expansion of dipole has two significant terms, and the computed coefficient for each of these terms should be made to approach the limit
have been divided by two so that the expansion does not duplicate the contributions to the radial component of the electric field. For example, in this Demonstration, the expansion of dipole has two significant terms, and the computed coefficient for each of these terms should be made to approach the limit 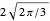 rather than
rather than  .
.
References
[1] D. J. Griffiths, Introduction to Electrodynamics, 3rd ed., Upper Saddle River, NJ: Prentice Hall, 1999.
[2] J. D. Jackson, Classical Electrodynamics, New York: Wiley, 1975.
Snapshots
Permanent Citation