Details

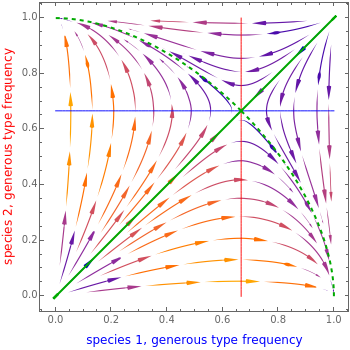
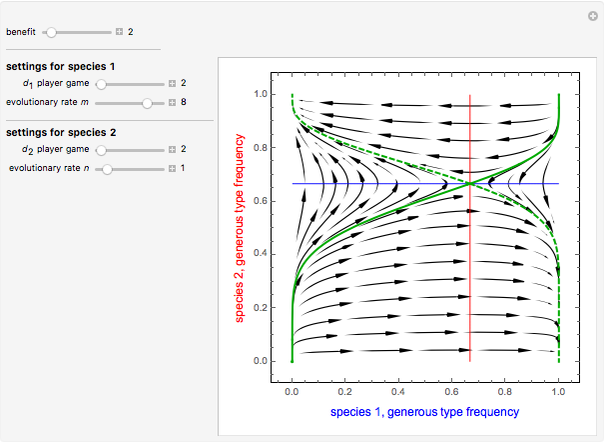
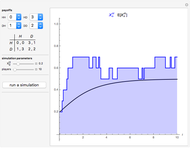
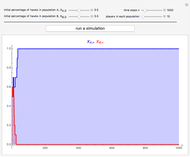
Snapshot 1: under equal player games and equal evolutionary rates, the basin of attractions of the interesting fixed points (1,0) and (0,1) are equal in size

Snapshot 2: for equal player games but unequal evolutionary rates, the slower-evolving species is at an advantage, as in this case species 2, where the basin of attraction of (1,0) is larger than (0,1)

Snapshot 3: forgoing dyadic interactions (now it is a five-player game) for the same inequality in evolutionary rates, the faster-evolving species is now at an advantage, as in this case species 1, where the basin of attraction of (0,1) is larger than (1,0), thus negating the Red King effect

The composition of both species can range from all selfish to all generous. If the other species is generous enough then selfish behavior is favored in both species. However, if the other species is selfish then it is advantageous to be generous. This concept is captured by the Snowdrift game. The favorable outcome for Species 1 is (0,1) as then it can be completely selfish while forcing the other species to be completely generous. The complementary favored outcome for species 2 is (1,0).

It was previously shown that if a species evolves slower then the basin of attraction of its favored outcome, it can increase in size. In this Demonstration it can be seen that this may not always be the case, hence forgoing the assumption of dyadic interactions, where the Red King effect does not necessarily persist. Instead, rich dynamics can be recovered due to the non-linear interactions of the growth rates and multiple number of players.

We make use of the Snowdrift game to illustrate the mutualistic scenario. In this case, each individual of each species has two strategies: to be generous or to be selfish. The payoffs for being generous and selfish are given by

and .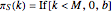

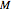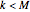In an interaction group, the "selfish" players get the benefit if the number of "generous" players is greater than or equal to the threshold . For the "generous" individuals, their effort is subtracted from the payoffs. The effort is shared if the quorum size is met, , but is in vain for . We set 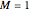for the Demonstration.

These payoffs are then converted to fitnesses of the two strategies. Summing over all possible compositions of groups, we arrive at the average fitnesses of the two strategies in species 1:

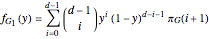and .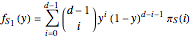

Following the same procedure for the two strategies in species 2 leads to the average fitness of the two species 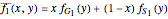and .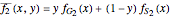

From this we can determine the change in the frequency of strategy 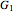and 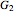via the replicator equations 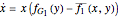and .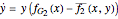

References

[1] C. T. Bergstrom and M. Lachmann, "The Red King Effect: When the Slowest Runner Wins the Coevolutionary Race," in Proceedings of the National Academy of Sciences, 100(2), 2003 pp. 593–598.

[2] G. S. Gokhale and A. Traulsen, "Mutualism and Evolutionary Multiplayer Games: Revisiting the Red King," in Proceedings of the Royal Society B: Biological Sciences, 279(1747), 2012 pp. 4611–4616.