Wolfram Demonstrations Project

13,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

Neighborhood Graphs with HITS and SALSA

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

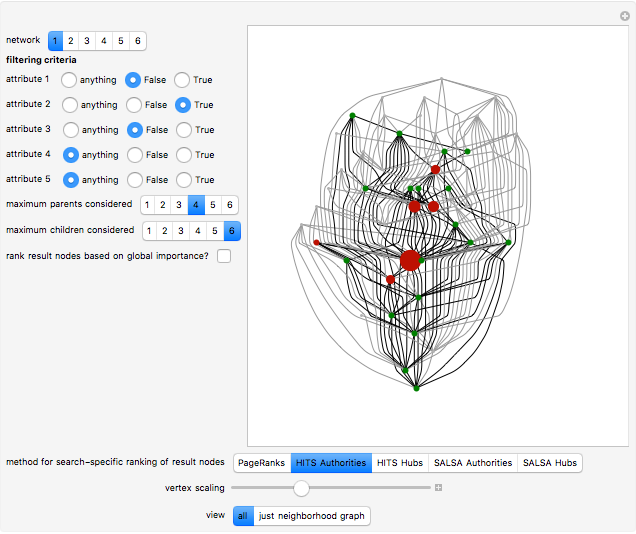
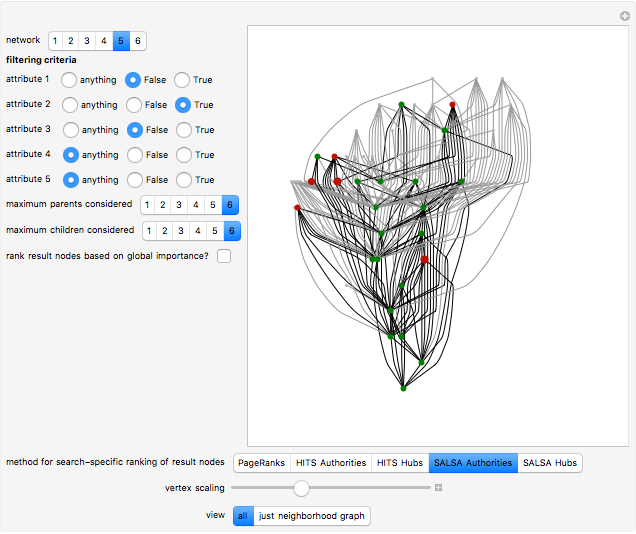
A particularly helpful search of a network such as the Internet or a citation network not only finds nodes that satisfy some criteria but also ranks those nodes for importance to create what amounts to a "reading list". Traditionally, this ranking was independent of the particular search performed. In part for reasons of speed, the nodes were ranked on the basis of their pre-computed importance within the entire network. More recently, however, relatively rapid algorithms have been developed to permit search-specific rankings. Thus, when these newer methodologies are used, if web pages or nodes in a citation network cover multiple topics and a particular document is important with respect to Topic A and far less important on Topic B, a search for documents based on the presence of Topic B will select this node but will not rank it highly. These newer methodologies essentially create a ranked and topic-specific "reading list" to explore the information revealed by the search. The key to these new methodologies is the creation of a "neighborhood graph", often containing far fewer nodes and edges than the full network to which various algorithms for computing node centrality can be rapidly applied.

[more]

This Demonstration shows how these new methods can create search-specific rankings of nodes selected by a search. It does so by the creation of a "neighborhood graph". You select from among six networks that are intended to resemble citation networks. Each node of the each network has an "attribute set" consisting of five Boolean values. You then filter the nodes (conduct a search) by choosing whether you want each member of the five attributes associated with the node to be True or False, or whether you don’t want to exclude any nodes based on the value of that attribute. These choices create a "result set" of nodes matching your selection. The Demonstration colors these nodes in red. These nodes are then augmented into a "base set" by adding a sample of the parents of each member of the result set and a sample of the children of each member of the result set. You specify the maximum cardinality of each selection of parents and the maximum cardinality of each selection of children. The base set thus establishes a partial "buffer" around the result set. The Demonstration colors these buffering nodes in green.

It is now time to determine how the nodes in the result set are to be ranked and the nodes are to be correlatively sized. Although you have the option of ranking the nodes based on their global importance in the entire network (using the traditional PageRanks method), in general, users will want to select a method for prioritizing the nodes in the result set based on the neighborhood graph. You can choose to prioritize the nodes in the neighborhood graph through the PageRanks method promoted by Google, the "HITS" (Hyperlink-Induced Topic Search) algorithm or the more recent "SALSA" (Stochastic Approach for Link Structure Analysis) algorithm. The latter two algorithms require you to specify whether you care about the nodes' importance as an "authority" relied on by other nodes or a "hub" that connects to an authoritative node.

Two additional controls let you customize the scale and the size of the vertices in the result set and permit you either to see the entire network or just the neighborhood graph.

[less]

Contributed by: Seth J. Chandler (March 2011)
Open content licensed under CC BY-NC-SA

Snapshots

Details

This Demonstration takes a few moments to initialize. Please be patient. It runs relatively swiftly thereafter.

The PageRanks method, the HITS algorithm, and the SALSA algorithm all use some "trickery" to ensure that computation of eigenvectors—a calculation that can be done quite swiftly on modern computers—correctly determines the stationary probabilities of node occupancy based on a random walk. This "trickery" is necessary because the Perron-Frobenius theorem guarantees that the computation of the principal eigenvector will correctly determine stationary probabilities when the underlying (adjacency) matrix is irreducible; yet, precisely because citation networks are at best weakly connected and may have multiple components, the adjacency matrix may be reducible. The PageRanks algorithm avoids the problem by ascribing "teleportation" to sink nodes. The HITS and SALSA algorithms essentially break the underlying adjacency matrix into irreducible submatrices and then weight the eigenvectors for each component based on the number of nodes in the corresponding component.

The parent and child nodes that compose the buffer are not exactly selected "at random" in this Demonstration. Rather, if you specify, for example, that you want each result node to have at most three parents, the Demonstration will select the first three parents it finds, which is in turn determined by the order in which the edges are listed in the underlying network. So the parents and children of each result node are selected arbitrarily, but not classically "at random".

This Demonstration achieves greater speed by creating a "LayeredGraphPlot" symbolic graphic for each of the networks that fix the coordinates for the nodes and then edges and then using substitution rules on these symbolic graphics to customize the graphic based on the computation requested by the user.

Key references for the HITS algorithm:

[1] J. Kleinberg, "Authoritative Sources in a Hyperlinked Environment," Journal of the ACM, 46(5), 1999 pp. 604–32.

[2] J. Miller, G. Rae, and F. Schaefer, "Modifications of Kleinberg's HITS Algorithm Using Matrix Exponentiation and Web Log Records," in Proceedings of the 24th Annual International ACM SIGIR Conference on Research and Development in Information Retrieval, New York: The Association for Computing Machinery, 2001 pp. 444–445.

[3] The HITS measure has been used to analyze the citation network created by United States Supreme Court decisions in E. Leicht, G. Clarkson, K. Shedden, and M. E. J. Newman, "Large-Scale Structure of Time Evolving Citation Networks," European Physical Journal B, 59(1), 2007 pp. 75–83.

Key references for the SALSA algorithm are

[4] R. Lempel and S. Moran, "The Stochastic Approach for Link-Structure Analysis (SALSA) and the TKC Effect," Computer Networks, 33(1–6), 2000 pp. 387–401.

[5] M. Najork, "Comparing the Effectiveness of HITS and SALSA," in Proceedings of the Sixteenth ACM Conference on Information and Knowledge Management, New York: The Association for Computing Machinery, 2007 pp. 157–164.

[6] A. Farahat, et. al., "Authority Rankings from HITS, PageRank, and SALSA: Existence, Uniqueness, and Effect of Initialization," SIAM Journal on Scientific Computing, 27(4), 2005 pp. 1181–1201.

[7] M. Jajork, S. Gollapundi, and R. Panigrahy, "Less is More: Sampling the Neighborhood Graph SALSA Better and Faster," in Proceedings of the Second ACM International Conference on Web Search and Data Mining, New York: The Association for Computing Machinery, 2009 pp. 242–251.

A PowerPoint presentation created by Adam Simkins (available at http://math.missouristate.edu/assets/Math/SALSA.ppt) is also particularly useful for explaining the SALSA algorithm.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send