Wolfram Demonstrations Project

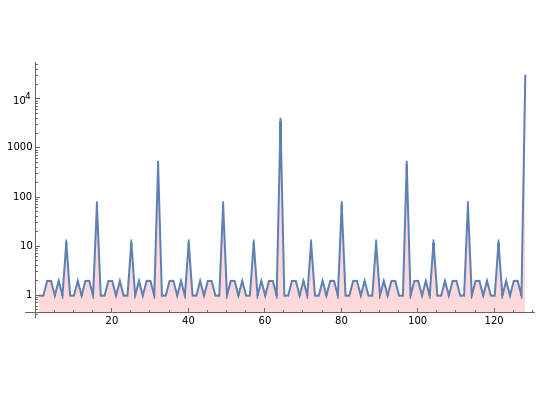
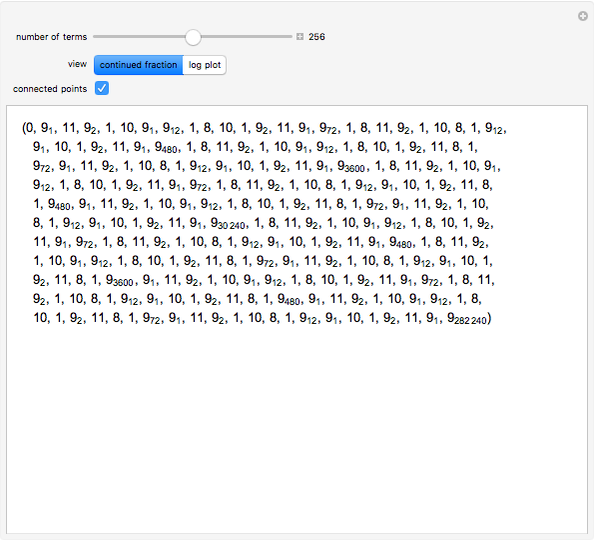
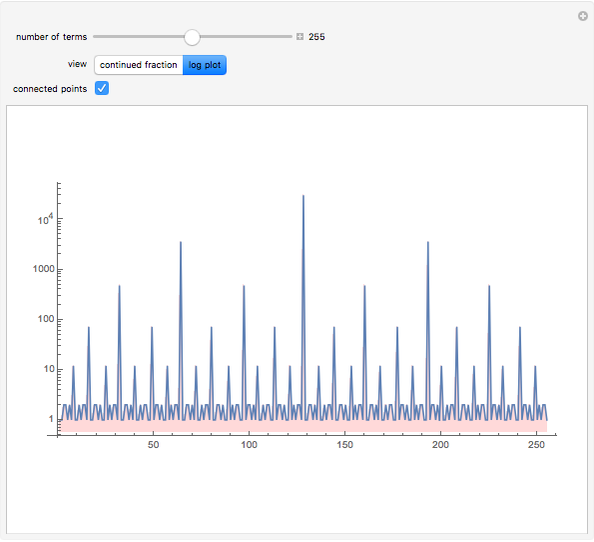
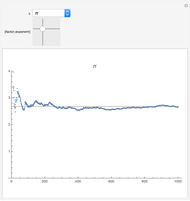
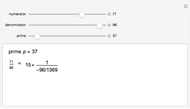
The Liouville constant is the transcendental number defined by

. Computing its continued fraction expansion in this semilog plot of the number of digits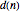

reveals the presence of sporadic large terms and a nested structure.

The notation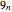

means an integer with

9's.

Interestingly, the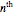

incrementally largest term (excluding the term

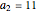) occurs precisely at positions

, and this term consists of (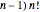

9's.

To compute the entries of this expansion the use of high-precision arithmetic is required; in this calculation, 500000-digit precision was used.

The more common way to represent a continued fraction is as follows:

but this is too wide to display for many terms.

This structure was found by the author.

Contributed by: Enrique Zeleny

Embed Interactive Demonstration New!

Just copy and paste this snippet of JavaScript code into your website or blog to put the live Demonstration on your site. More details »

Nested Structure of the Continued Fraction of Liouville's Constant