Net and Gross Reserve of Life Insurance

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
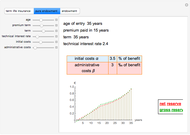
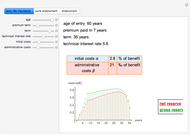
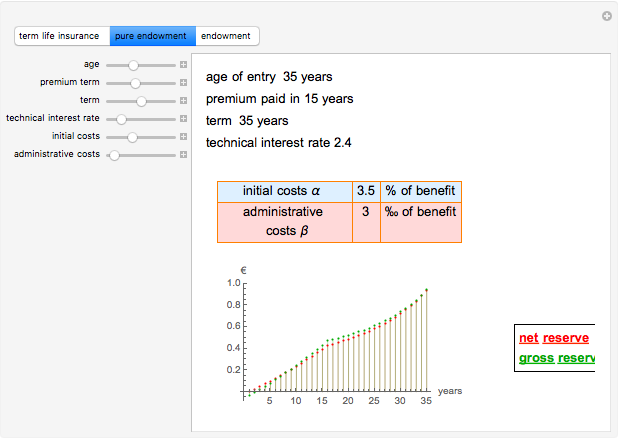
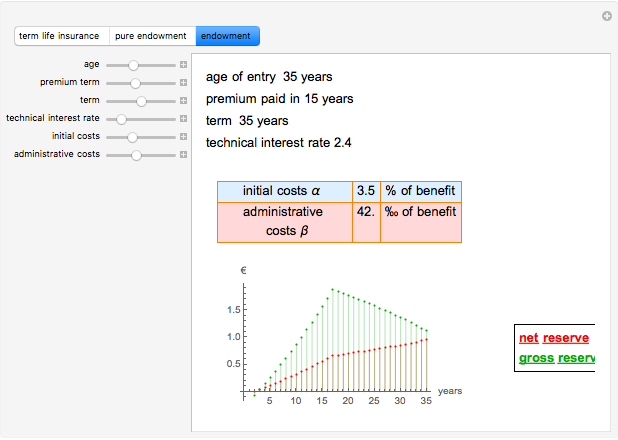
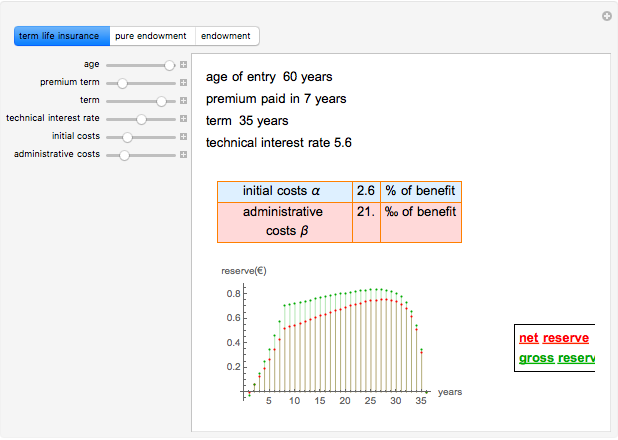
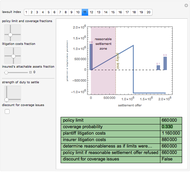
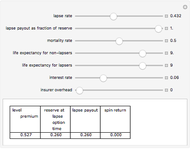
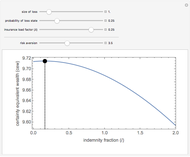
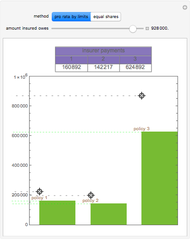
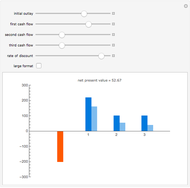
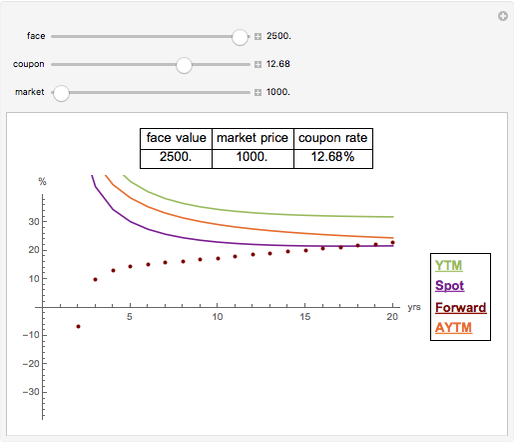
This Demonstration shows the net and gross premium reserves of life insurance. The reserves are calculated for the three basic types of life insurance: term insurance, pure endowment, and endowment with unitary benefit. For all cases, the premium can be paid as an  -year temporary annuity. You can vary the technical interest rate in the range from 1 to 10% per annum. The decremental data used for the calculations is 2001–2005 Czech Republic data.
-year temporary annuity. You can vary the technical interest rate in the range from 1 to 10% per annum. The decremental data used for the calculations is 2001–2005 Czech Republic data.
Contributed by: Gergely Nagy (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Term life insurance is the basic insurance product where the insurance event is the death of the insured. For pure endowment, the insurance event is the survival of the term. The endowment is a mixture of the two other types of insurance.
The net reserve of endowment for  years, where the premium is paid in
years, where the premium is paid in 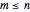 years, is:
years, is:
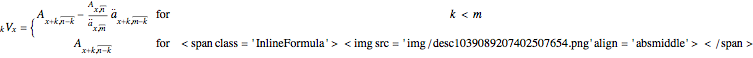
( is used for the more standard
is used for the more standard 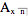 actuarial notation.)
actuarial notation.)
Assuming the initial costs to be 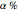 of the benefit, the administrative costs
of the benefit, the administrative costs 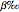 of the benefit, and the collection fee
of the benefit, and the collection fee  of the gross premium (but as follows the result does not depend on
of the gross premium (but as follows the result does not depend on  ), we can calculate the gross premium as
), we can calculate the gross premium as
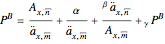 ,
,
then the gross reserve is
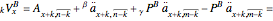


where

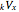 is the net reserve in time
is the net reserve in time  ,
,
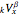 is the gross reserve in time
is the gross reserve in time  ,
,
 is the endowment for
is the endowment for  years,
years,
 is the annual premium paid within
is the annual premium paid within 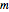 years.
years.
The calculation of reserves for term insurance and pure endowment is analogous, using 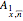 for term life insurance and
for term life insurance and 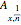 for pure endowment.
for pure endowment.
The computation is based on the commutation functions:
 ,
,
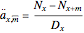 ,
,
where 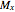 ,
, 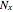 , and
, and 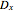 can be derived using the decremental data
can be derived using the decremental data 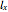 and
and  :
:
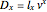 and
and 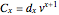 ,
,
 and
and 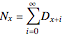 ,
,
where
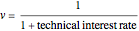 .
.
Permanent Citation