Wolfram Demonstrations Project

13,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

Nets for Cowley's Dodecarhombus and Related Solids

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

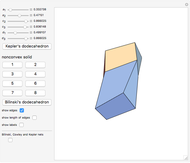
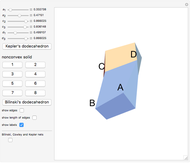
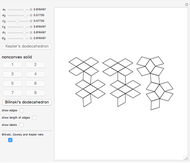
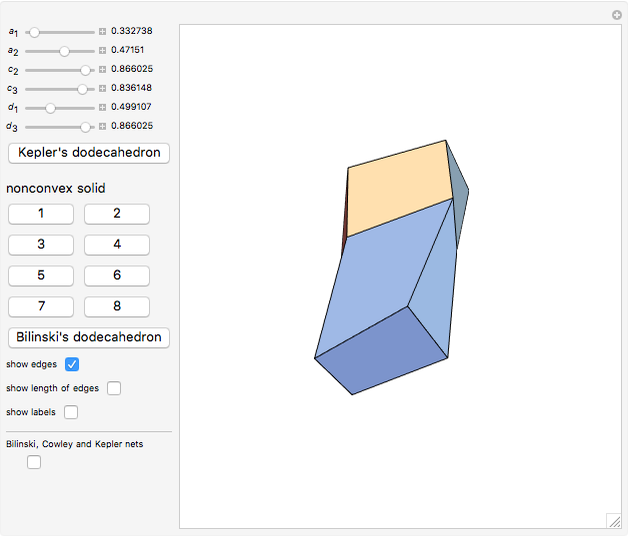
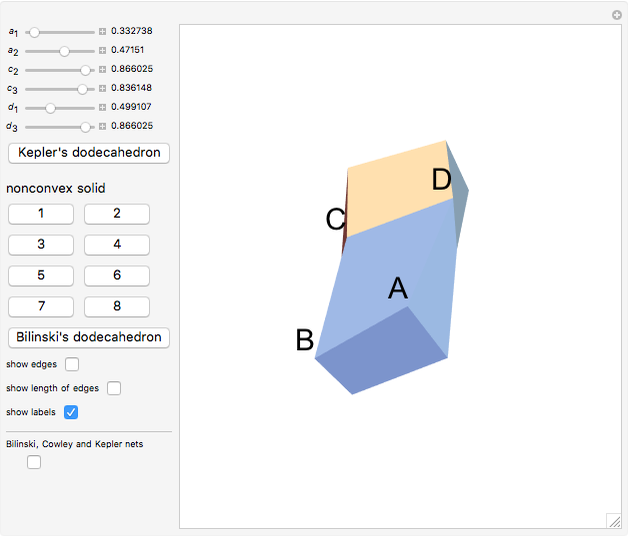
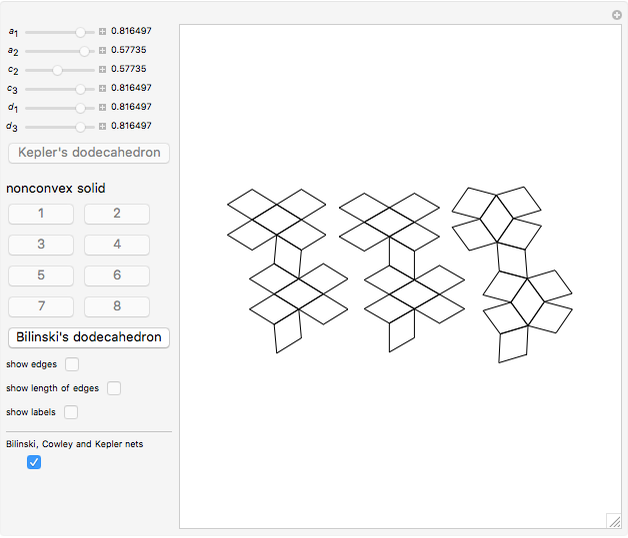
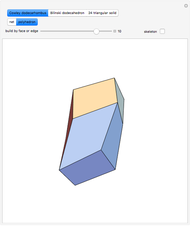
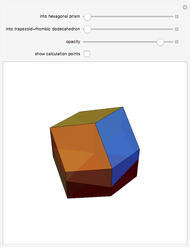
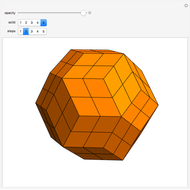
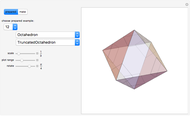
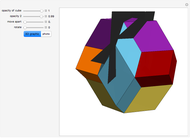
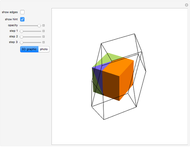
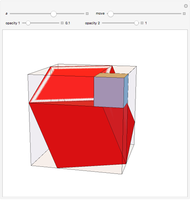
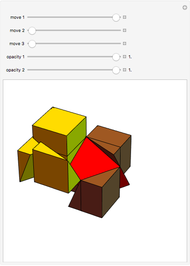
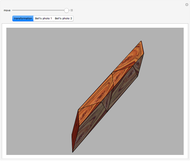
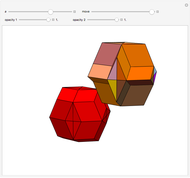
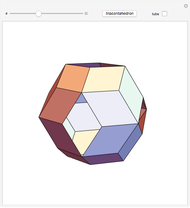
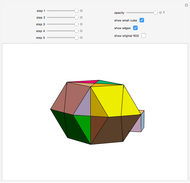
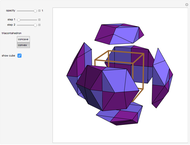
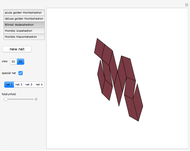
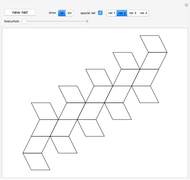
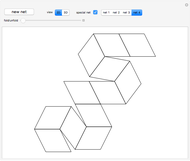
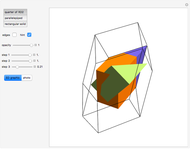
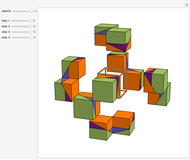
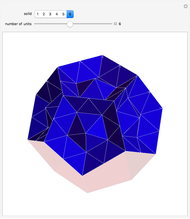
This Demonstration shows that Cowley's net can be folded into eight nonconvex solids with nonplanar faces.

[more]

A dodecarhombus is a solid figure having twelve rhomb faces. In [1, pp. 2–3] and [3, p. 22], it was shown that Cowley's dodecarhombus net [3, p. 23] did not consist of golden rhombuses (Bilinski) nor of rhombuses of a rhombic dodecahedron (Kepler). So it cannot be folded into a convex polyhedron. But if we consider Cowley's rhombuses as hinged equilateral triangles, his net can be folded into a nonconvex polyhedron. So in this case, rhombuses are a kind of skeleton in the sense of [4, p. 282], although not all dihedral angles are congruent. Creases can also be made along larger diagonals of 60° rhombuses or along combinations of both types.

[less]

Contributed by: Izidor Hafner (August 2018)
Open content licensed under CC BY-NC-SA

Details

There is an extensive discussion of Cowley's dodecarhombus net in [5, pp. 76–80]. The net in [1, p. 3] of a rhombic dodecahedron of the second kind (Bilinski's dodecahedron) was made by Hafner and was part of an internet discussion mentioned in [3, p. 22], where it supported Hafner's claim that Cowley's net was not a net of a rhombic dodecahedron of the second kind.

References

[1] "Rombski poliedri." (Dec 17, 2018) www.logika.si/revija/Stare-revije/revija15-5.pdf.

[2] J. L. Cowley, Geometry Made Easy: A New and Methodical Explanation of the Elemnets [sic] of Geometry, London: Mechell, 1752.

[3] B. Grünbaum. "The Bilinski Dodecahedron, and Assorted Parallelohedra, Zonohedra, Monohedra, Isozonohedra and Otherhedra." (Dec 17, 2018) digital.lib.washington.edu/researchworks/bitstream/handle/1773/15593/Bilinski_dodecahedron.pdf.

[4] P. R. Cromwell, Polyhedra, New York: Cambridge University Press, 1997.

[5] M. Friedman, A History of Folding in Mathematics: Mathematizing the Margins, New York, NY: Springer Berlin Heidelberg, 2018.

Snapshots

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send