Newtonian Gravitational Wave Chirp Signal from Merger of a Compact Binary

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
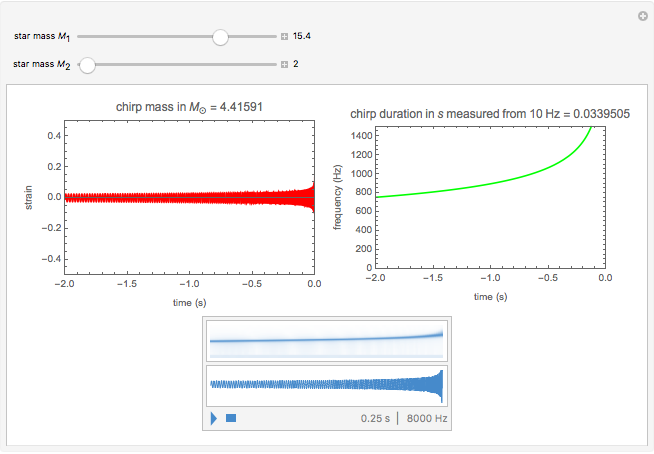
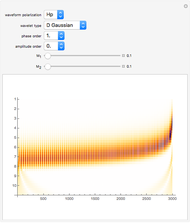
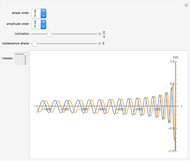
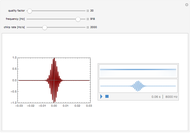
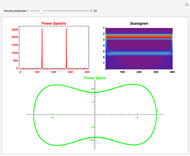
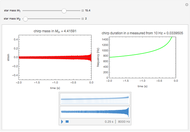
This Demonstration shows the gravitational wave emitted before the merger of two compact objects orbiting around each other, such as a neutron star and a black hole. Only the leading-order Newtonian approximation is considered. The waveform is a chirp, which consists of increasing wave amplitude with time (first figure) and increasing frequency with time (second figure). The chirp can be heard by playing the sound of the waveform.
Contributed by: Satya Mohapatra (September 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
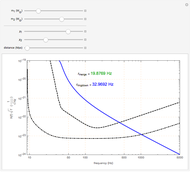
When orbiting compact binary objects are approaching each other, the resulting gravitational wave can be described with the leading-order Newtonian chirp waveform. This waveform depends only on:
the chirp mass  , where
, where 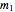 and
and 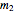 are the component masses of the binary system, and
are the component masses of the binary system, and
the distance of the binary from the point of observation.
We assume that the distance of the binary from the point of observation is 1 Mpc. The chirp duration measured from 10 Hz to the frequency of merger is smaller for more massive binary objects.
Reference
[1] M. Maggiore, Gravitational Waves, Oxford: Oxford University Press, 2008.
Permanent Citation
"Newtonian Gravitational Wave Chirp Signal from Merger of a Compact Binary"
http://demonstrations.wolfram.com/NewtonianGravitationalWaveChirpSignalFromMergerOfACompactBin/
Wolfram Demonstrations Project
Published: September 13 2011