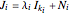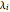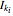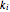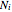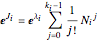Nilpotent Matrices in Jordan Decompositions
Initializing live version

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
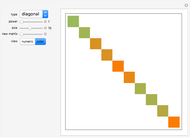
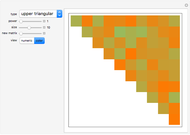
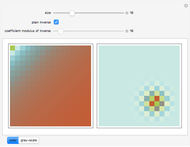
In this representation, the greener the square, the larger the entry relative to the others.
[more]
Contributed by: Pablo Alberca Bjerregaard (University of Malaga, Spain) and George Beck (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
detailSectionParagraphPermanent Citation
"Nilpotent Matrices in Jordan Decompositions"
http://demonstrations.wolfram.com/NilpotentMatricesInJordanDecompositions/
Wolfram Demonstrations Project
Published: March 7 2011