No-Four-In-Plane Problem

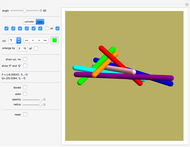
In a 3×3×3 grid, select eight points so that no four points are in a plane. Ignoring rotations and reflections, the solution is unique. Extending the problem to a 4×4×4 grid, 10 points can be placed in at least 211 distinct ways so that no four points are in a plane. Visually, this implies that cylinders only intersect at the endpoints. Whether 11 points can be placed, if more distinct solutions exist, or how many points can be placed on the 5×5×5 grid for no-four-in-plane remain unsolved problems.