Nodal Points in Bohmian Mechanics

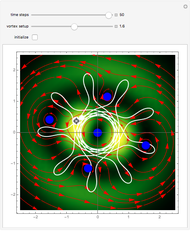
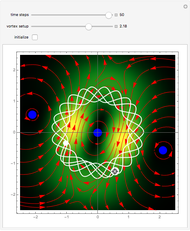
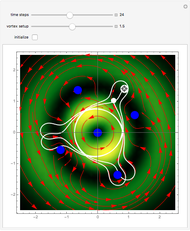
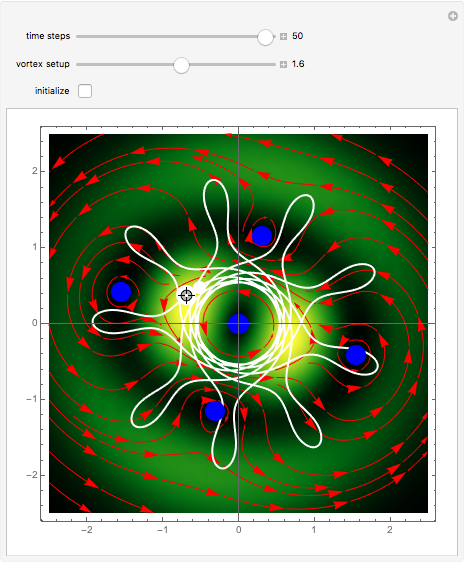
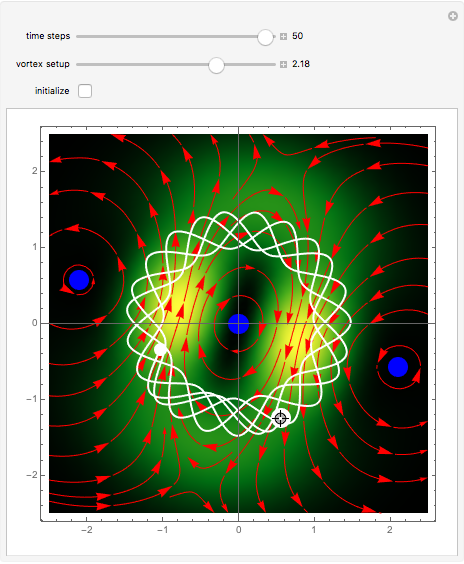
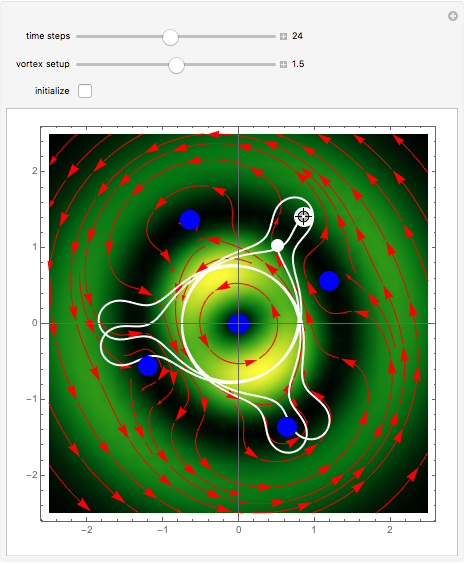
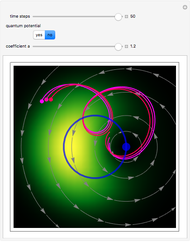
Moving vortices or nodal points play an important role in testing the attributes of quantum motion in the framework of the de Broglie–Bohm trajectory method [2]. This Demonstration studies an unnormalized superposed wavefunction for the two-dimensional harmonic oscillator. Chaos emerges from the sequential interaction between the quantum path with the moving nodal points, depending on the distance and the frequencies between the quantum particles and their initial positions. Here, chaotic motion means the exponential divergence of initially neighboring trajectories (see Related Links below). Vortices are readily formed in several different scenarios, including the superposition of quantum states [1, 2]. 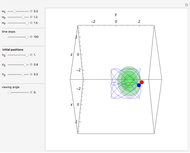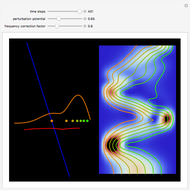Although the initial quantum state contains only one or three nodal points, depending on the value, during the time evolution new vortices are created and annihilated, so that at certain times there are at most five vortices present. If , there is a nodal region and the squared wavefunction becomes time-independent. In the vicinity of the vortices, the velocity vector field becomes circular and the trajectory is very unstable. The trajectories of the vortices are periodic. The Bohmian trajectory forms periodic, quasi-periodic, or chaotic curves while interacting with the nodal points. The graphic shows the trajectory (white), the velocity vector field (red), the nodal points (blue), the absolute wavefunction, and the initial and end point (white) of the trajectory. You can return to the original settings with the "initialize" checkbox.