Wolfram Demonstrations Project

12,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

Nonlinear Coupled Oscillator

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

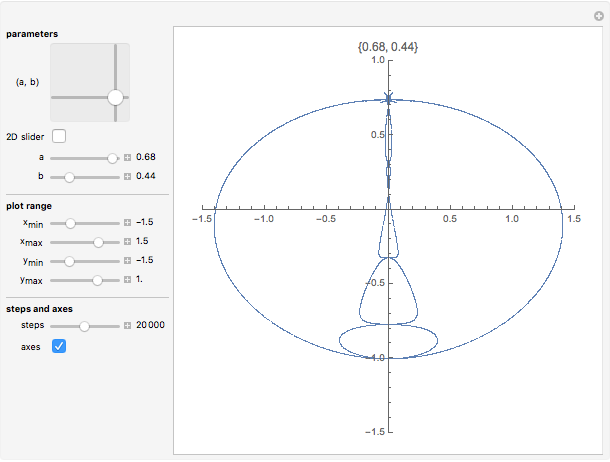
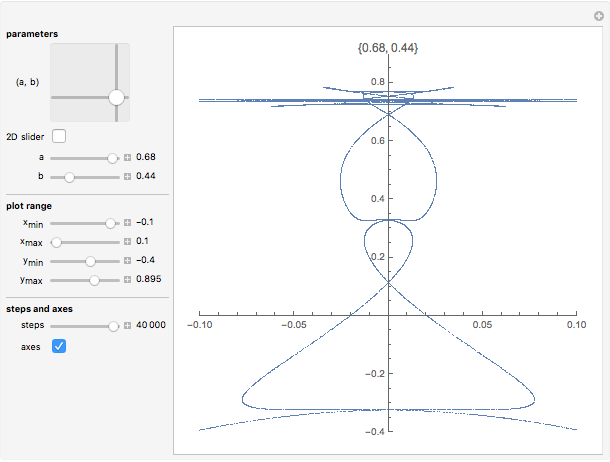
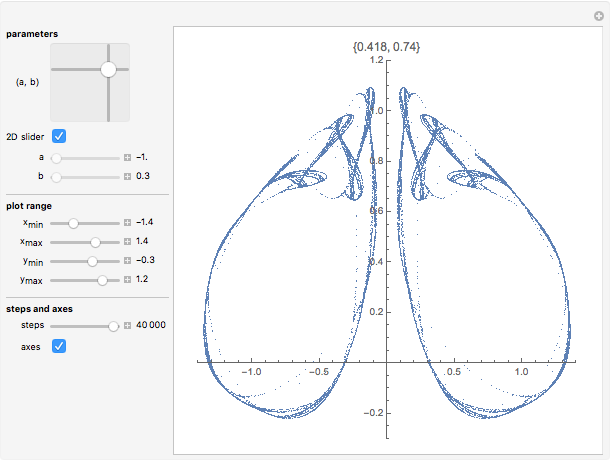
The recurrence equations constitute a two-parameter canonical form of a nonlinear coupled oscillator.

Contributed by: Ralf Schaper (March 2011)
Open content licensed under CC BY-NC-SA

Snapshots

Details

More information is in the following two papers.

W. Metzler, W. Beau, W. Frees, and A. Ueberla, "Symmetry and Self-Similarity with Coupled Logistic Maps," Zeitschrift fur Naturforschung, 42(3), 1987 pp. 310–318.

W. Metzler, A. Brelle, and K. D. Schmidt, "Nonanalytic Dynamics for Generating the Mandelbrot Set: A Tutorial," International Journal of Bifurcation and Chaos, 2(2), 1992 pp. 241–250.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send