Normal Distribution with Continued Fractions

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
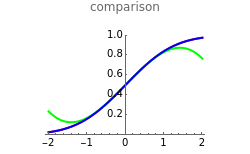
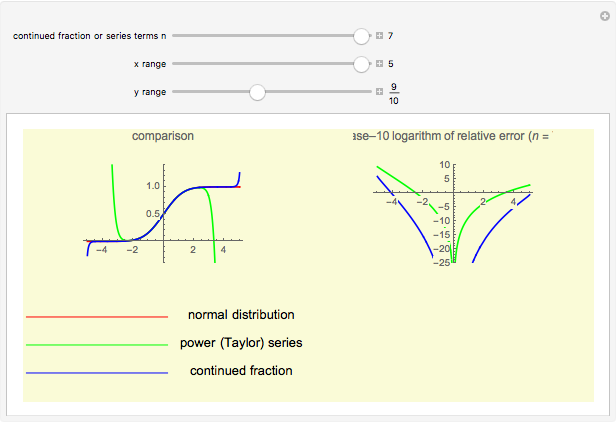
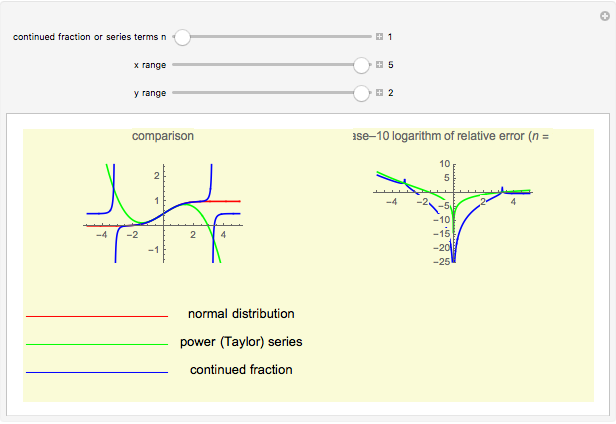
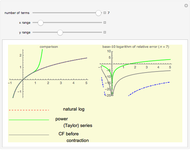
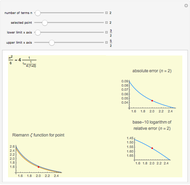
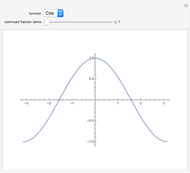
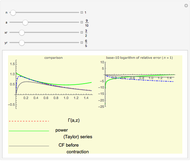
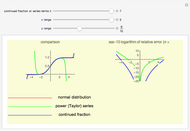
Continued fractions provide a very effective toolset for approximating functions. Usually the continued fraction expansion of a function approximates the function better than its Taylor or Fourier series. This Demonstration compares the quality of two approximations to the normal distribution. One is the Taylor series and the other is a continued fraction expansion the author has developed as a canonical even contraction based on a continued fraction expansion from Shenton.
Contributed by: Andreas Lauschke (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
By dragging the first slider for the number of terms used in the expansions, you can clearly see that the Taylor series makes hardly any progress. The terms in the Taylor polynomial become progressively more complicated; higher terms have huge numbers in the numerator and denominator and in the exponent, but the contribution of this "expense" becomes quite stale.
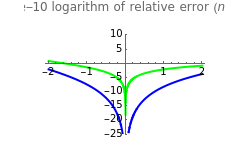
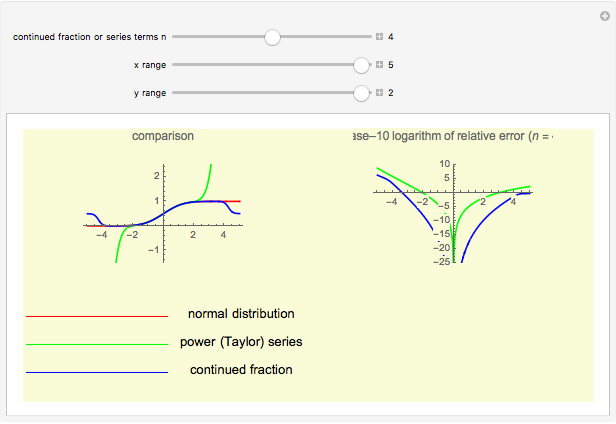
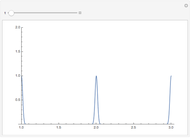
The continued fraction expansion approximates the normal distribution much better, by several orders of magnitude, as can be seen in the log-plot of the relative errors. However, it has two poles when  is odd (no poles when
is odd (no poles when  is even), but the deviation caused by the poles is quite narrow, and where they occur, the error of the Taylor series expansions is equally unacceptable. Additionally, the poles move further away from 0 as
is even), but the deviation caused by the poles is quite narrow, and where they occur, the error of the Taylor series expansions is equally unacceptable. Additionally, the poles move further away from 0 as  increases. (It is generally a shortcoming of polynomials that for larger
increases. (It is generally a shortcoming of polynomials that for larger 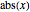 they cannot approximate functions well that converge toward constants, as polynomials tend to
they cannot approximate functions well that converge toward constants, as polynomials tend to 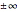 as
as 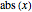 becomes large. Rational function approximation—for example using continued fractions or Padé approximations—or certain special functions can perform this much better.)
becomes large. Rational function approximation—for example using continued fractions or Padé approximations—or certain special functions can perform this much better.)
Additional Information:
The algorithm uses the backward recurrence method to compute the continued fraction expansion. This method has been shown to be extremely stable for most continued fraction expansions, which is extremely important on numerical platforms that incur truncation or roundoff error due to the limitations of machine precision. It can be shown that the backward recurrence method (from tail to head) is vastly more stable (and even self-correcting) than the forward recurrence method (from head to tail) for two important classes of continued fractions: the Stieltjes continued fractions (which include the C-fractions) and those that fulfill the parabolic convergence region theorem. Several function classes with known Stieltjes continued fraction expansions include exponential integrals, incomplete gamma functions, logarithms of gamma functions, the error function, ratios of successive Bessel functions of the first kind, and Euler's hypergeometric function, as well as various elementary transcendental functions. The forward recurrence method (which solves a second-order linear difference equation), however, can be computationally more efficient due to the carryover of results from one step to the next, which is a property the backward recurrence method does not possess.
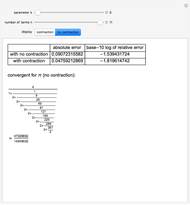
Although the terms in the canonical contraction are more complex than the ones in Shenton's continued fraction expansion, the speed gain on traditional numerical platforms (Java, .Net, C) is enormous. In Mathematica the differences of the timing results of the canonical contraction and Shenton's original continued fraction expansion are immaterial (which is a further example of the superior paradigms Mathematica provides when Compile and functional programming symbols such as Fold are used). The following uses 10,000 uniformly distributed random numbers between -2 and 2 and outputs the computation time depending on up to 20 steps (42 in the non-contracted method). The design of the canonical contraction requires only Floor[n/2]-1 steps to produce the same number when  steps are used in Shenton's original continued fraction expansion, so
steps are used in Shenton's original continued fraction expansion, so 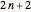 steps are used for nds below to ensure the non-contracted method attains the same accuracy.
steps are used for nds below to ensure the non-contracted method attains the same accuracy.
Table[{First@ Timing@Do[nd[n, RandomReal[{-2, 2}]], {10000}], First@Timing@Do[nds[2 n + 2, RandomReal[{-2, 2}]], {10000}]}, {n, 20}] // TableForm
with
nds = Compile[{{n, _Integer}, x}, 1 - 1/(Sqrt[2 Pi]) (Sqrt[Pi/2] - Exp[-1/2 x^2] x/(1 + Fold[#2[[1]]/(#2[[2]] + #1) &, 0, Transpose[{Table[(-1)^(k) k x^2, {k, n, 1, -1}], Table[(2 k + 1), {k, n, 1, -1}]}]]))];
and nd from the initialization code of the Demonstration.
However, when Java is used (standard Java on the client VM, no tweaking of runtime parameters on the server VM) the acceleration the canonical contraction provides is quite dramatic. The following uses 100,000 uniformly distributed random numbers between -2 and 2 and outputs the computation time depending on up to 20 steps (i.e., 42 steps in the non-contracted method).
import java.util.Random; public class normdist { final static double pi=Math.PI; final private static double shenton(final double x,final int steps) { double res=0; for (int i = steps; i > 0; i--) { res = Math.pow(-1,i)*i *x*x/ ((2*i+1) + res); } return 1 - 1/(Math.sqrt(2*pi))* (Math.sqrt(pi/2) - Math.exp(-0.5 * Math.pow(x,2))*x/(1 +res)); } final private static double contracted(final double x,final int steps) { double res=0; for (int i = steps-1; i > -1; i--) { res = ((2*(27 + 57*i + 38*i*i + 8*i*i*i))*x*x*x*x/(5 + 4*i))/((63 + 64*i + 16*i*i)-((7 + 4*i) *x*x/(5 + 4*i)) + res); } return 1 - 1/(Math.sqrt(2*pi))* (Math.sqrt(pi/2) - Math.exp(-0.5 * Math.pow(x,2))*x/(1 -5*x*x/(15 + 2*x*x+res))); } final public static void main(String[] args) { Random generator = new Random(); long t1, t2, t3, t4; double r, ratio; for (int n = 0; n < 20; n++) { t1 = System.currentTimeMillis(); for (int i = 0; i < 100000; i++) { r = generator.nextDouble(); shenton(4 * r - 2, 2*n+2); } t2 = System.currentTimeMillis(); t3= t2-t1; System.out.println("n: "+n+", Method: Shenton, Milliseconds: " + t3); t1 = System.currentTimeMillis(); for (int i = 0; i < 100000; i++) { r = generator.nextDouble(); contracted(4 * r - 2, n); } t2 = System.currentTimeMillis(); t4= t2-t1; ratio=(double)t3/t4; System.out.println("n: "+n+", Method: Contraction, Milliseconds: " + t4+", Ratio: "+ratio); } } }
You can clearly see that with an increase in precision (larger  ) the runtime of the canonical contraction method is only a fraction of the runtime of the non-contracted method.
) the runtime of the canonical contraction method is only a fraction of the runtime of the non-contracted method.
The backward recurrence method of the continued fraction expansion is also more stable than its conversion to a Padé approximation (even when several forms of the HornerForm of the numerator and denominator polynomials are used), as can easily be verified with several sample cases using the Java and Mathematica programs shown here.
Permanent Citation