Normal Sections and Gauss Map for the Hyperbolic Paraboloid

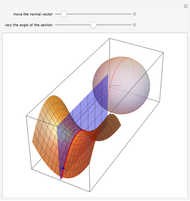
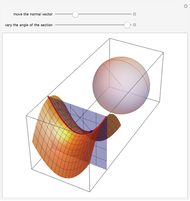
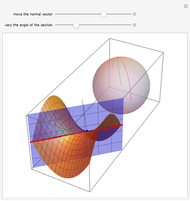
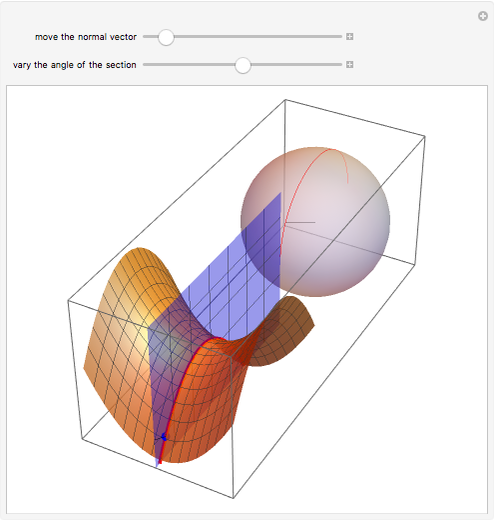
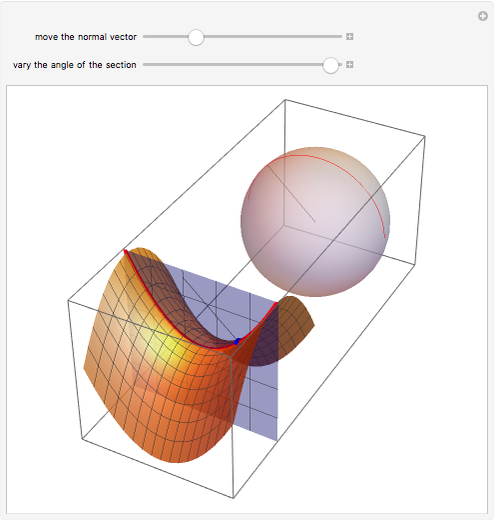
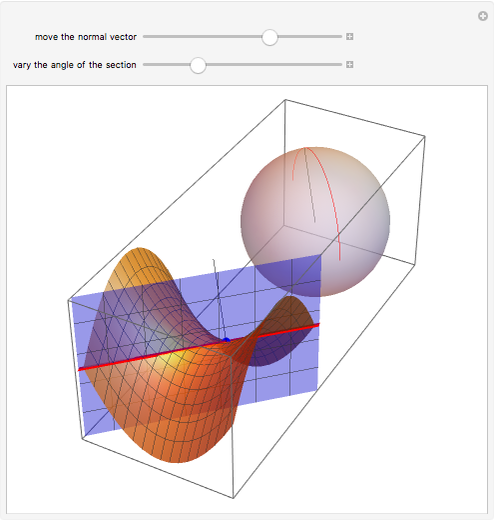
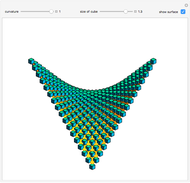
The curve that is the intersection of the hyperbolic paraboloid with an orthogonal plane is called the normal section. The Gauss map assigns to each point on the surface its unit normal vector, which lies on the unit sphere. This Demonstration shows that the image of a normal section of the hyperbolic paraboloid at the origin under the Gauss map is an arc of a great circle on the sphere.