Nowhere-Neat Squaring the Square

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
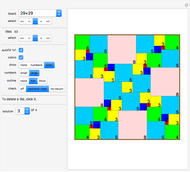
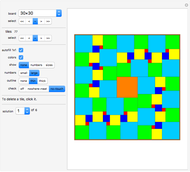
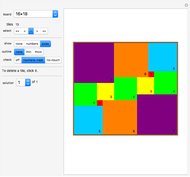
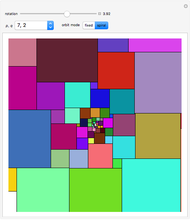
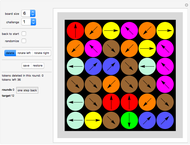
The goal is to completely tile a large square area with smaller squares such that no two tiles have a side in common ("nowhere-neat tiling").
[more]
Contributed by: Karl Scherer (October 2008)
Additional contributions by: Patrick Hamlyn and Joseph DeVincentis
Open content licensed under CC BY-NC-SA
Snapshots
Details
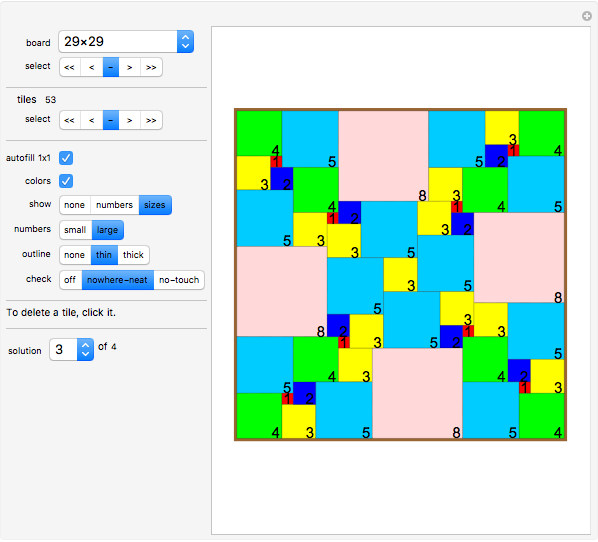
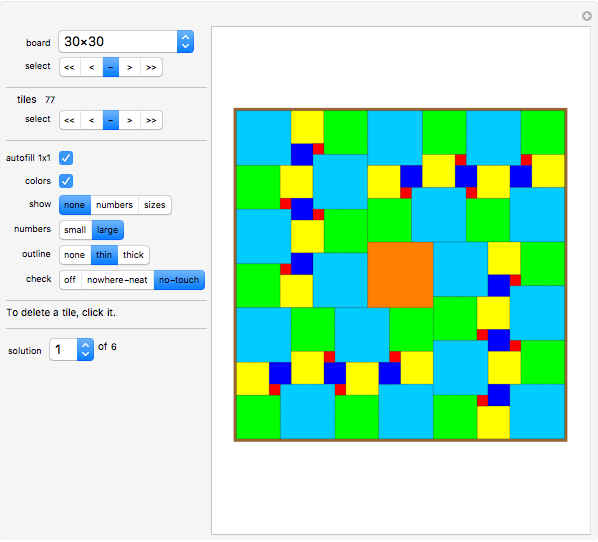
Click the board to specify the position of the bottom-right corner of a square. The program will automatically draw the largest possible square that fits.
The "board" pop-up menu lets you choose the size of the square board.
The "select" setter-bar also lets you select the size of the square board.
In the next row the number of square "tiles" is displayed.
The "select" setter-bar lets you go back to the first square tile, one move back, one move forward or jump to the last stored move.
Click "autofill 1x1" to have the system automatically fill in 1x1 square tiles where no other tiles can go.
Click "color" to show the tiles in color or just white.
Click the "show" setter-bar to show the size for each square tile or its sequence number or neither.
Click the "numbers" setter bar to show the numbers in 10 points size or 15 points size.
Click the "outline" setter-bar to display thick or thin outlines of the square tiles or no outline at all.
Click an existing square tile to remove it from the board.
The following sizes of squares have a nowhere-neat tiling with smaller squares:
11×11, 16×16, 18×18, 19×19, 20×20 and all 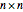 with
with  . Additionally, the tiling can always be chosen to be fault-free and to contain the unit square as a tile.
. Additionally, the tiling can always be chosen to be fault-free and to contain the unit square as a tile.
Click the "check nowhere-neat" button to get a warning whenever this rule is violated by a newly added tile.
Click the "check no-touch" button to get a warning whenever this rule is violated by a newly added tile.
In both cases, the system will only check the newest tile; so it is advisable to click these buttons before you start. Therefore the "check nowhere-neat" button is clicked at the start of this Demonstration.
The "solution" pop-up menu lets you select a solution to the current problem. Most board sizes have more than one solution.
History:
The general nowhere-neat problem was solved by the author in February 2001. A similar theorem on no-touch tilings was also found by the author at the same time. These theorems were published in the Journal of Recreational Mathematics.
In 2005 the author also proved similar theorems for squaring rectangles. The proofs of these theorems are attached to the Zillions game, "Square The Rectangle". There you will also find tilings (where they exist) for all rectangles up to size 50×50.
References:
[1] K. Scherer, New Mosaics, privately published, 1997.
[2] K. Scherer, "Square The Square," "Square The Square II," "Square The Rectangle," "Square The Square Solver," Zillions of Games, www.zillions-of-games.com.
[3] K. Scherer, "A General Theorem on No-Touch Tilings of Squares and a General Theorem on Nowhere-Neat Tilings of Squares," Journal of Recreational Mathematics, 32(1), 2003–2004 pp. 1–13.
Permanent Citation
"Nowhere-Neat Squaring the Square"
http://demonstrations.wolfram.com/NowhereNeatSquaringTheSquare/
Wolfram Demonstrations Project
Published: October 13 2008