Nuclear Magnetic Resonance Spectrum of Ethanol

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
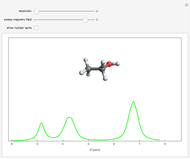
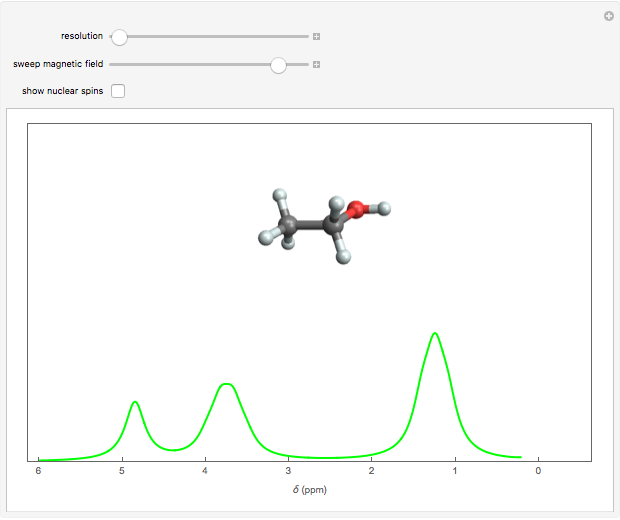
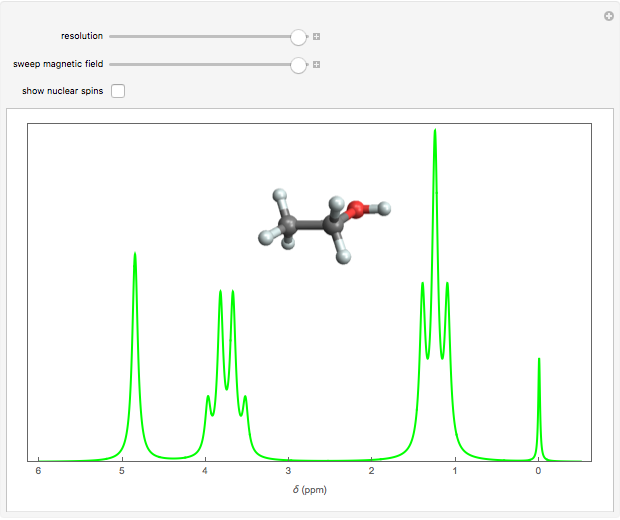
Nuclear magnetic resonance (NMR) spectroscopy can measure radio-frequency Zeeman transitions of proton spins in a magnetic field. It is more convenient to sweep the magnetic field through the resonances at a fixed frequency, typically 60 MHz. The resonances are sensitive to the chemical environment of nonequivalent protons, an effect known as the chemical shift. A classic example is the ethanol molecule C C
C OH, which shows three chemically-distinct hydrogen atom sites, thus three NMR peaks with intensity ratios 3:2:1. The relevant parameter is
OH, which shows three chemically-distinct hydrogen atom sites, thus three NMR peaks with intensity ratios 3:2:1. The relevant parameter is  , representing the fractional deviation of the chemical shift measured in parts per million (ppm) from that of tetramethylsilane (TMS), a convenient standard assigned the reference value
, representing the fractional deviation of the chemical shift measured in parts per million (ppm) from that of tetramethylsilane (TMS), a convenient standard assigned the reference value  . A small amount of TMS is often added to the sample being measured to calibrate the
. A small amount of TMS is often added to the sample being measured to calibrate the  -scale.
-scale.
Contributed by: S. M. Blinder (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Snapshot 1: the earliest detection of the chemical shift, obtained at Stanford University in 1951; the three peaks in ethanol have approximate  values of 4.85, 3.75 and 1.25, with relative intensities identifying these with the OH, C
values of 4.85, 3.75 and 1.25, with relative intensities identifying these with the OH, C , and C
, and C protons, respectively
protons, respectively
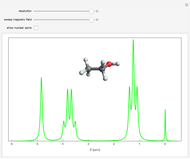
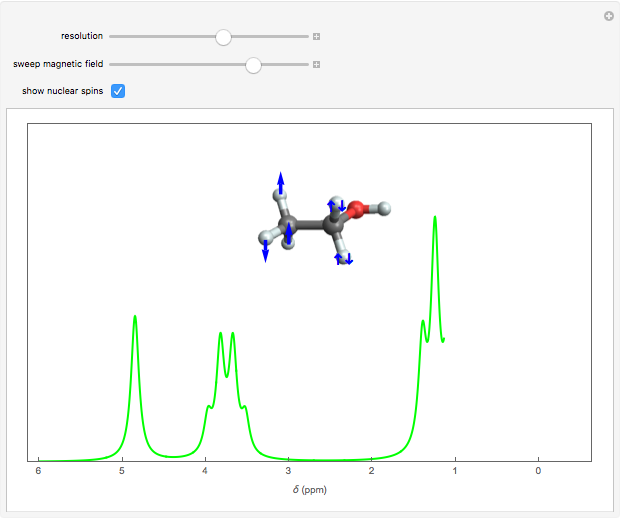
Snapshot 2: at higher resolution, spin-spin splittings can be observed; the peak at  is from a trace amount of TMS
is from a trace amount of TMS
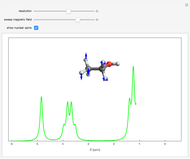
Snapshot 3: resonance absorption and emission of protons in the C group; the different possible orientations of the C
group; the different possible orientations of the C protons are also indicated
protons are also indicated
Reference: S. M. Blinder, Introduction to Quantum Mechanics, Amsterdam: Elsevier, Academic Press, 2004 p. 247ff.
Permanent Citation