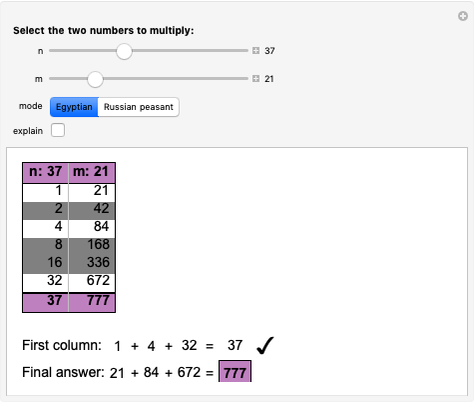
Numbers as Sets

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
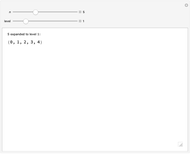
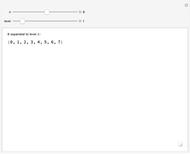
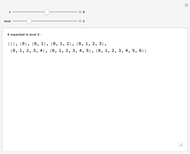
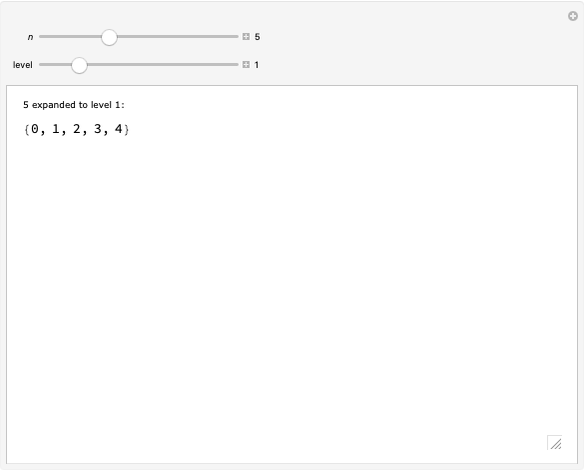
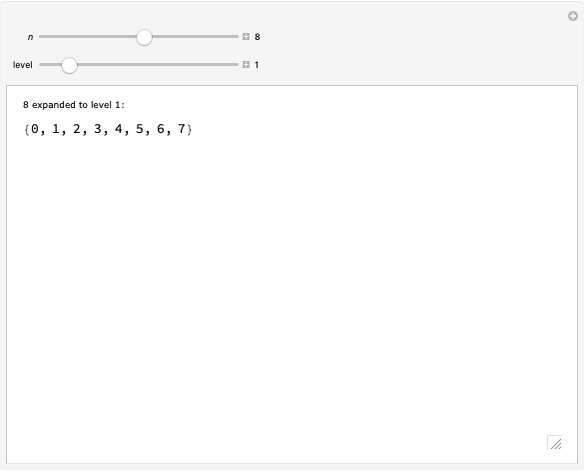
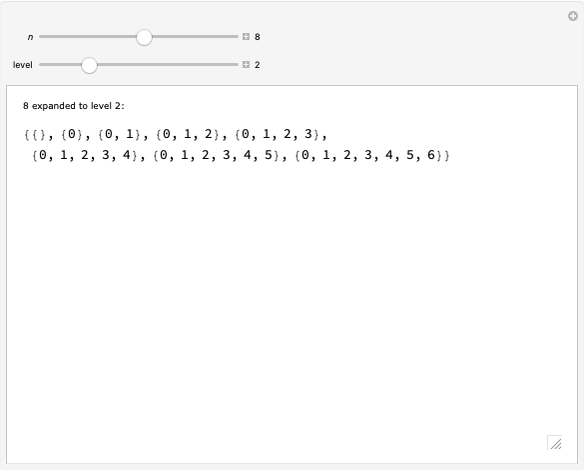
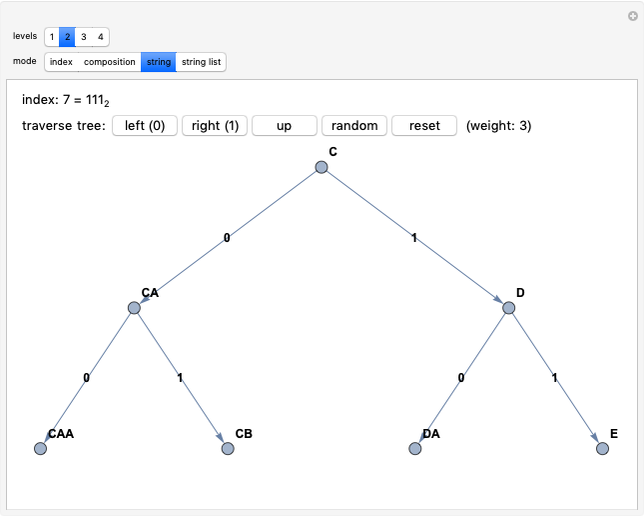
Every child naturally learns how to count, but few non-mathematicians know that the "whole numbers" 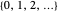 have been rigorously defined in terms of sets: each ordinal number is defined as the ordered set of all smaller ordinals. This Demonstration visually unpacks this recursive definition for the first few ordinals, letting you select an ordinal number
have been rigorously defined in terms of sets: each ordinal number is defined as the ordered set of all smaller ordinals. This Demonstration visually unpacks this recursive definition for the first few ordinals, letting you select an ordinal number 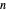 and specifying how many levels deep the translation should be applied.
and specifying how many levels deep the translation should be applied.
Contributed by: Kenneth E. Caviness (May 2012)
Open content licensed under CC BY-NC-SA
Snapshots
Details
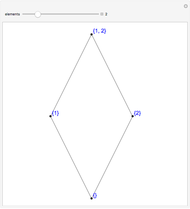
The definition of the ordinal numbers (whose finite members are the whole numbers) was originally due to Georg Cantor, whose groundbreaking treatment extended to transfinite numbers. The standard definition of the ordinals, due to John von Neumann, defines each ordinal as the well-ordered set of all smaller ordinals. Thus  , since no previous ordinals have been defined, and then
, since no previous ordinals have been defined, and then 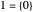 ,
, 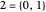 , and in general,
, and in general, 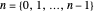 .
.
A succinct recursive version of this definition is 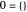 ,
, 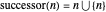 . This gives the same results as above; for example,
. This gives the same results as above; for example,  .
.
It is interesting to note that this definition is not limited to finite numbers. Set theorists define the first transfinite number as 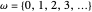 , and continue far beyond this "smallest infinity".
, and continue far beyond this "smallest infinity".
Permanent Citation