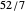Numerical Flowers
Initializing live version

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
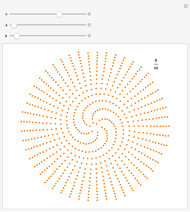
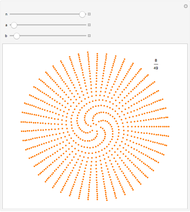
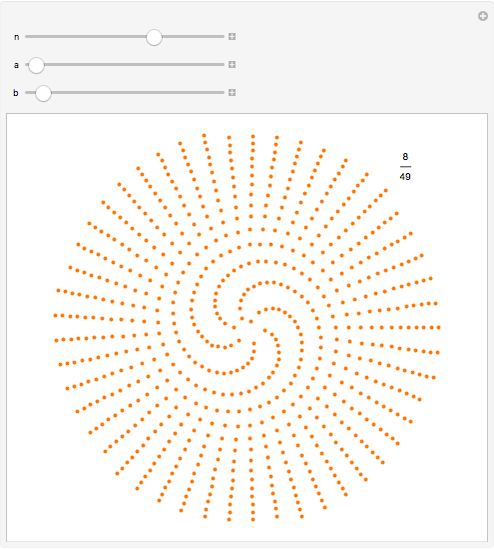
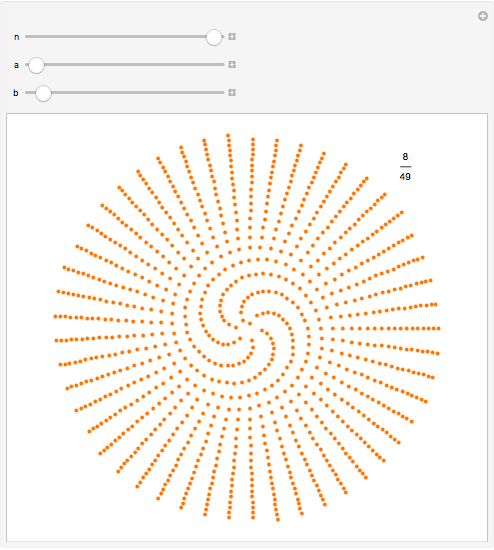
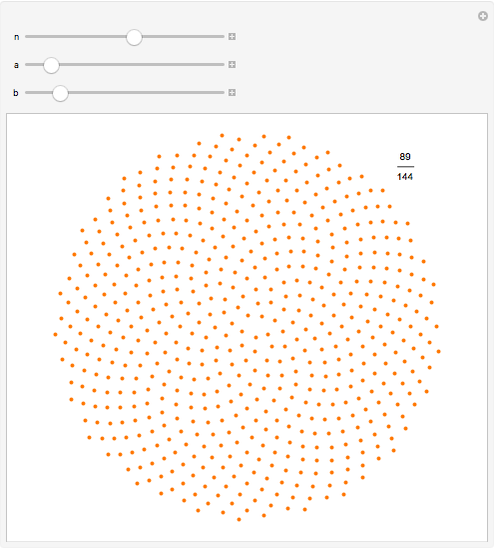
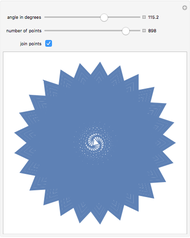
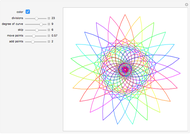
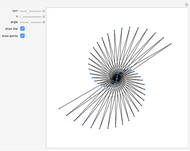
This generalizes how seeds are distributed on plants such as sunflowers. Starting from the center, each successive seed is a fixed distance from the previous seed and is rotated from the line connecting the previous two seeds by a constant angle. Using the controls, you can explore how different angles, 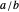 , produce varying patterns with
, produce varying patterns with 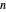 seeds.
seeds.
Contributed by: Ken Levasseur (UMass Lowell) (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
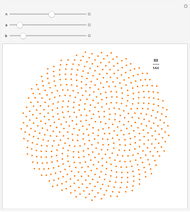
M. Naylor, "Golden, 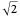
 , and
, and 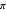 Flowers: A Spiral Story," Mathematics Magazine, 75(June), 2002 pp. 163-172.
Flowers: A Spiral Story," Mathematics Magazine, 75(June), 2002 pp. 163-172.
Permanent Citation