Numerical Inversion of the Laplace Transform: The Zakian Method

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
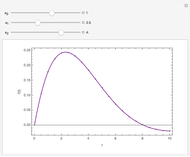
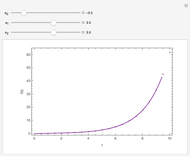
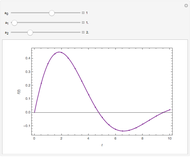
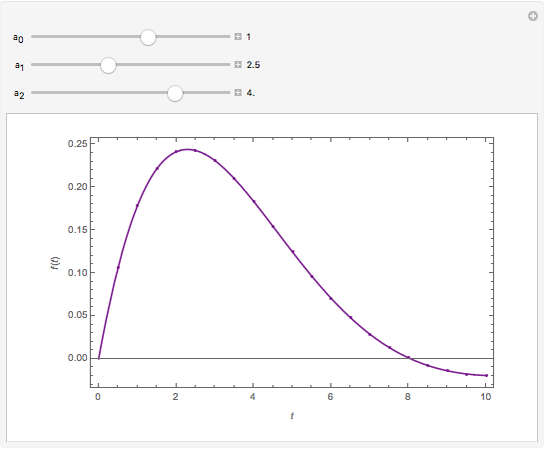
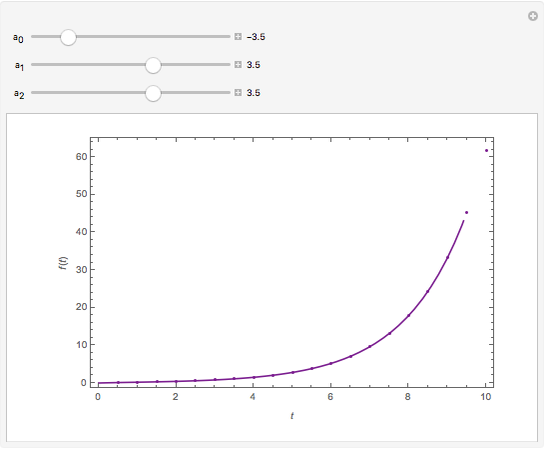
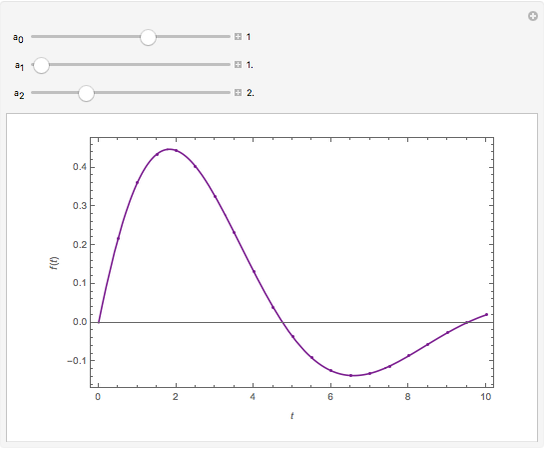
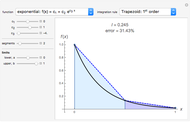
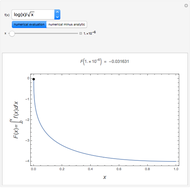
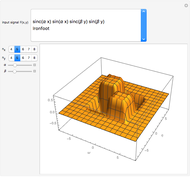
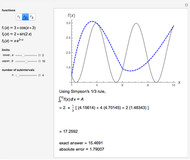
This Demonstration shows how to numerically invert the Laplace transform 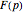 of a simple function
of a simple function 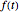 :
: 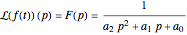 , where you can set
, where you can set 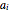 for
for 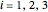 . The magenta curve is the analytical inverse function obtained with the help of the built-in Mathematica function InverseLaplaceTransform and the blue dots are the selected values of the numerical inverse of
. The magenta curve is the analytical inverse function obtained with the help of the built-in Mathematica function InverseLaplaceTransform and the blue dots are the selected values of the numerical inverse of  . It is clear that the Zakian method performs well for this kind of test function.
. It is clear that the Zakian method performs well for this kind of test function.
Contributed by: Housam Binous (March 2011)
Open content licensed under CC BY-NC-SA
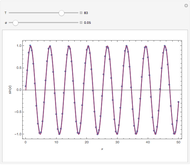
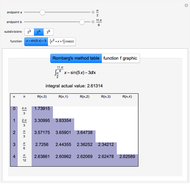
Snapshots
Details
The Zakian method uses the following formula in order to invert  :
:
 , where
, where 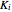 and
and 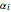 are the tabulated constants for the Zakian method.
are the tabulated constants for the Zakian method.
R. G. Rice and D. D. Do, Applied Mathematics and Modeling for Chemical Engineers, New York: Wiley, 1995.
Permanent Citation