Numerical Iso-Optic Curve of the Ellipse

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
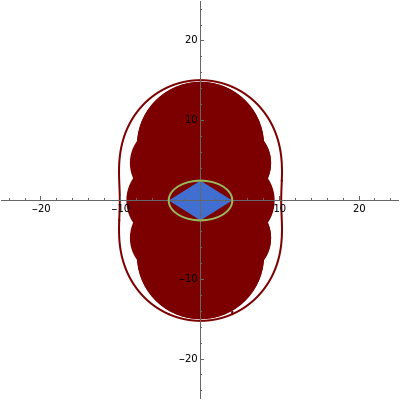
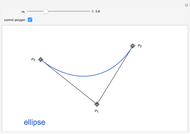
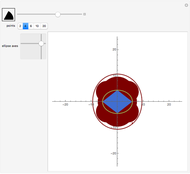
This Demonstration shows how the iso-optic curve of the ellipse can be approximated by the iso-optic curve of the polygon circumscribing it.
Contributed by: Géza Csima (Budapest University of Technology and Economics) (December 2009)
Additional contributions by: János Tóth
Suggested by: Jenő Szirmai
Open content licensed under CC BY-NC-SA
Snapshots
Details
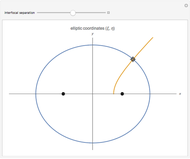
The iso-optic of a curve is formed from the points from which the given curve subtends the angle  . This Demonstration is based on two previous ones (see the first two Related Links), but here we approximate the ellipse with polygons as a way to find its iso-optic curve.
. This Demonstration is based on two previous ones (see the first two Related Links), but here we approximate the ellipse with polygons as a way to find its iso-optic curve.
You can chose some discrete values of  from the range between
from the range between  and
and 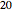 . Using the other controls, you can set the semi-minor and semi-major axes of the ellipse between
. Using the other controls, you can set the semi-minor and semi-major axes of the ellipse between  and
and  and the angle
and the angle  between
between 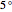 and
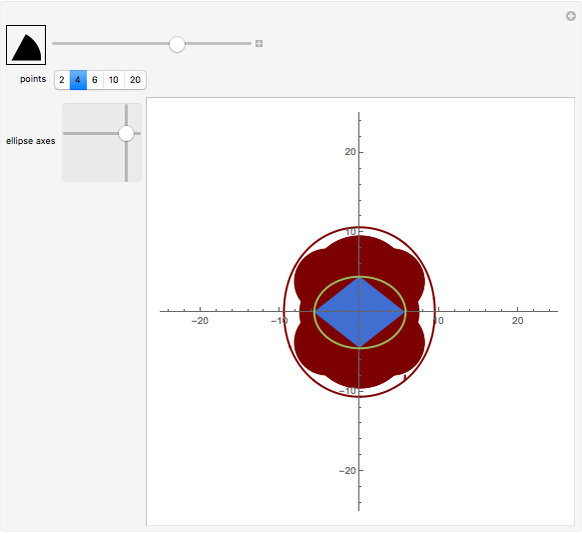
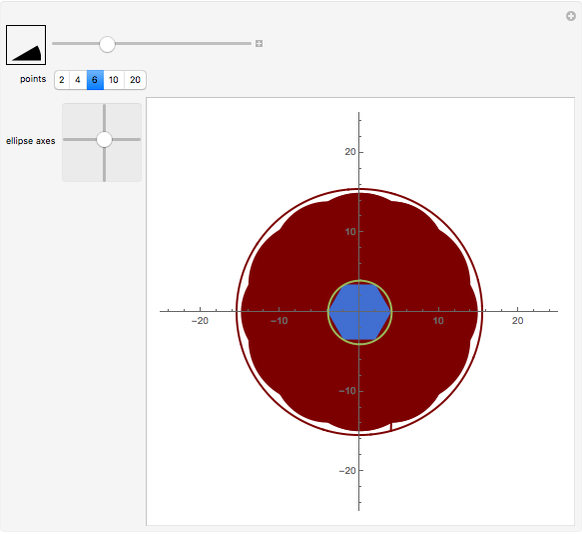
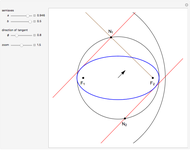
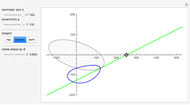
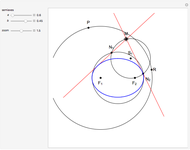
and 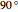 . The ellipse is green and the inscribed polygon is blue (except in the case
. The ellipse is green and the inscribed polygon is blue (except in the case  ). The red domains show the points from which the polygon (and also the ellipse) subtends an angle greater than or equal to
). The red domains show the points from which the polygon (and also the ellipse) subtends an angle greater than or equal to  and its boundary are the points from which the ellipse subtends the angle
and its boundary are the points from which the ellipse subtends the angle  . We have already proved that this curve is the correct solution of this problem.
. We have already proved that this curve is the correct solution of this problem.
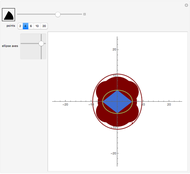
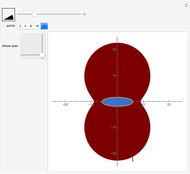
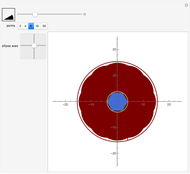
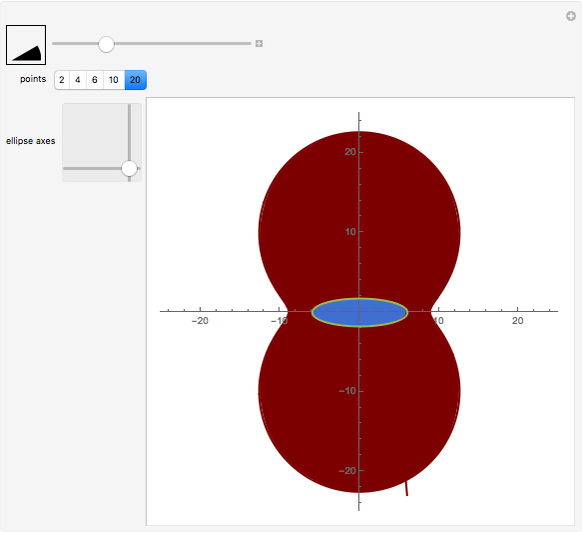
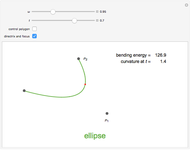
The snapshots show some general situations, except the second one, which shows that if we set  large enough, the iso-optic curve of the polygon (which is the boundary of the red domain) is almost the iso-optic curve of the ellipse.
large enough, the iso-optic curve of the polygon (which is the boundary of the red domain) is almost the iso-optic curve of the ellipse.
Permanent Citation