Wolfram Demonstrations Project

12,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

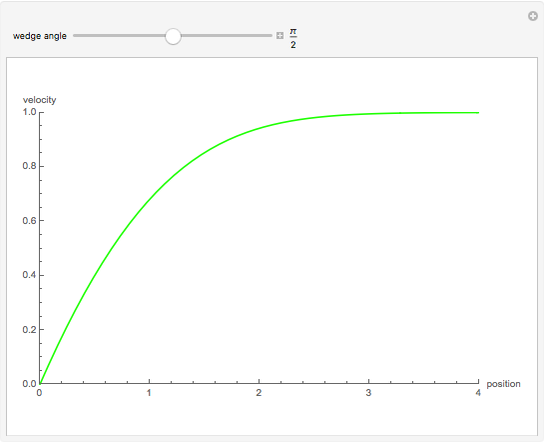
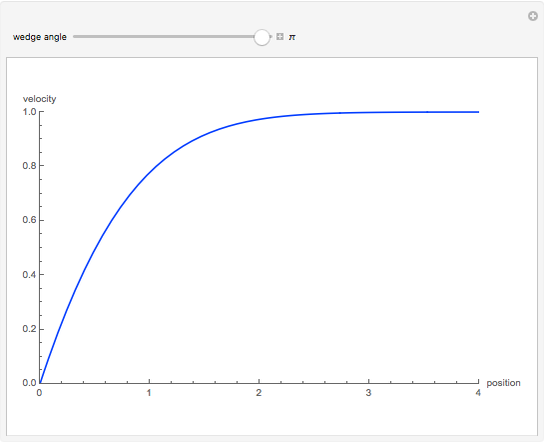
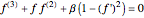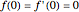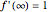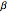Numerical Solution of the Falkner-Skan Equation for Various Wedge Angles

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

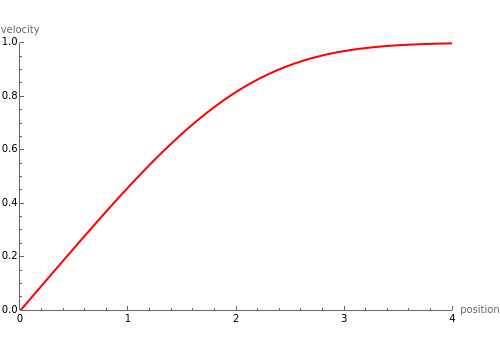
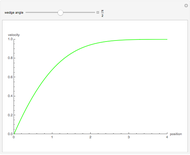
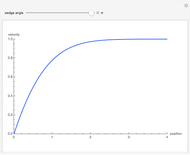
The flow past a wedge is governed by the Falkner-Skan equation:

[more]

with and .

This equation admits only a numerical solution, which requires the application of the shooting technique.

This Demonstration plots the velocity for various wedge angles. The well-known Blasius equation appears as a particular case in this study; it represents the flow past a flat plate (when the wedge angle is zero). Planar stagnation flow is also treated by setting the wedge angle to .

[less]

Contributed by: Housam Binous (March 2011)
Open content licensed under CC BY-NC-SA

Snapshots

Details

W. M. Deen, Analysis of Transport Phenomena, New York: Oxford University Press, 1998.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send