Octahedral Rotational Symmetry Types

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
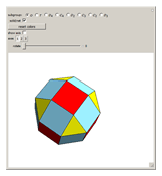
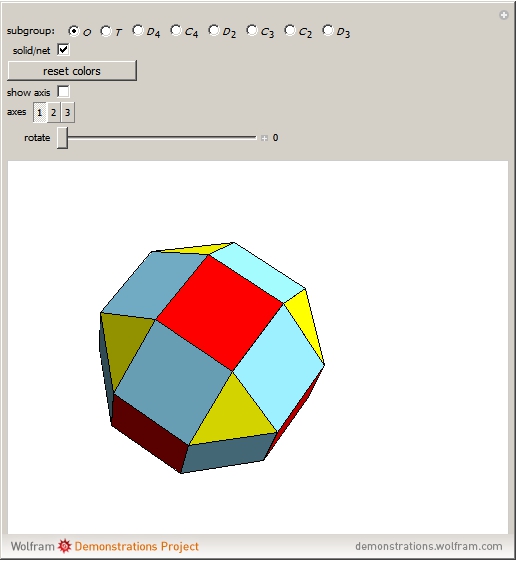
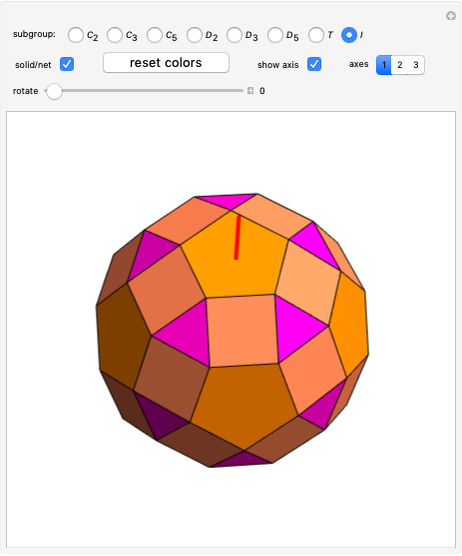
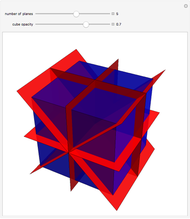
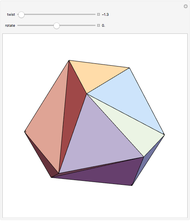
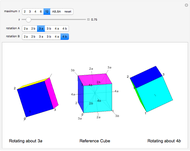
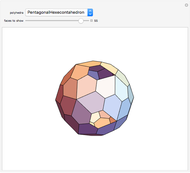
This Demonstration colors the faces of the small rhombicosidodecahedron to show the subgroups of the octahedral rotational group. Faces that are e.g. blue land on another blue face when one of the group transformations is applied.
Contributed by: Izidor Hafner (June 2014)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Reference
[1] P. R. Cromwell, Polyhedra, New York: Cambridge University Press, 1997 pp. 309–313.
Permanent Citation
"Octahedral Rotational Symmetry Types"
http://demonstrations.wolfram.com/OctahedralRotationalSymmetryTypes/
Wolfram Demonstrations Project
Published: June 3 2014