Omitted Variable Bias

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
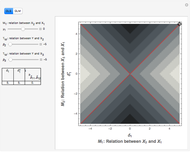
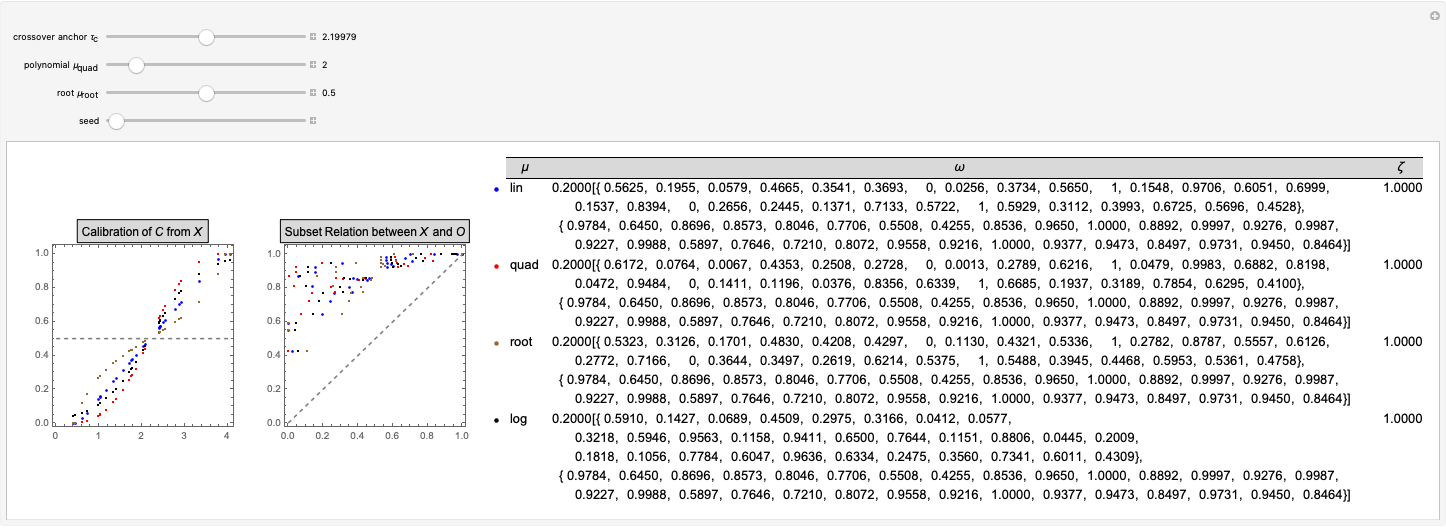
In social science research, control variables are often included out of concerns about inducing bias into the coefficients of interest [1, 2]. However, short of knowing the true data-generating process—an unlikely situation—the inclusion of even relevant controls may in fact aggravate the problem.
[more]
Contributed by: Alrik Thiem (December 2010)
After work by: Kevin A. Clarke, University of Rochester (USA)
Open content licensed under CC BY-NC-SA
Snapshots
Details
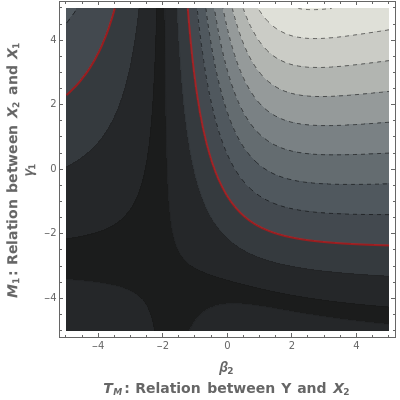
For the case of OLS, let 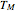 be the true model,
be the true model,  be first misspecified model, and
be first misspecified model, and  be the second misspecified model.
be the second misspecified model.
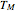 :
: 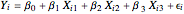 , with
, with 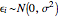 ,
,
 :
: 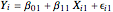 , and
, and
 :
: 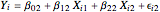 .
.
If for  we have
we have 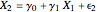 , then
, then 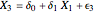 .
.
If for  we have
we have  , then the bias
, then the bias  of the expected values of
of the expected values of  for
for  and
and  for
for  are given by
are given by
(1)  ,
,
(2)  .
.
According to the logic of including controls in order to reduce bias, the following weak inequality should always hold.
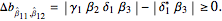
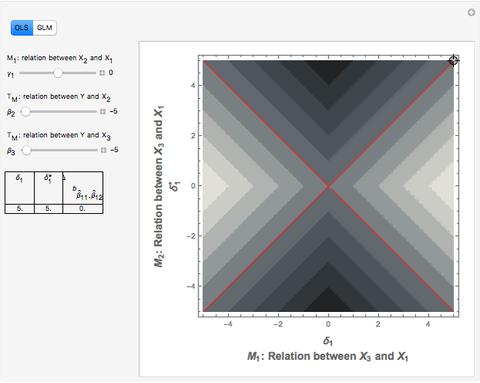
For the case of GLM, as before let 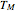 be the true model, let
be the true model, let  be the first misspecified model, and let
be the first misspecified model, and let  be the second misspecified model.
be the second misspecified model.
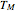 :
: 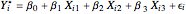 , with
, with 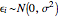 and
and 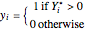 ,
,
 :
: 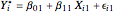 , and
, and
 :
: 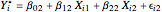 .
.
The normalized values of 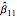 and
and 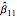 are given by [1] as
are given by [1] as
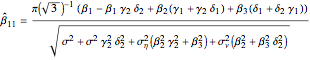 and
and
 .
.
According to the logic of including controls in order to reduce bias, the following weak inequality should always hold.
 .
.
References
[1] K. A. Clarke, "Return of the Phantom Menace: Omitted Variable Bias in Political Research," Conflict Management and Peace Science, 26(1), 2009 pp. 46–66.
[2] K. A. Clarke, "The Phantom Menace: Omitted Variable Bias in Econometric Research," Conflict Management and Peace Science, 22(4), 2005 pp. 341–352.
[3] M. H. Gail, S. Wieand, and S. Piantadosi, "Biased Estimates of Treatment Effect in Randomized Experiments with Nonlinear Regressions and Omitted Covariates," Biometrika, 71(3), 1984 pp. 431–444.
[4] J. S. Cramer, Logit Models from Economics and Other Fields, Cambridge: Cambridge University Press, 2003.
Permanent Citation