On the Fundamental Theorem of Phyllotaxis
Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
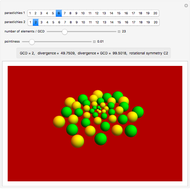
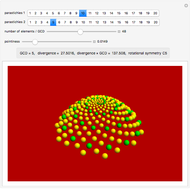
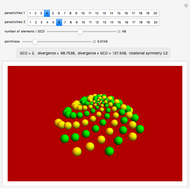
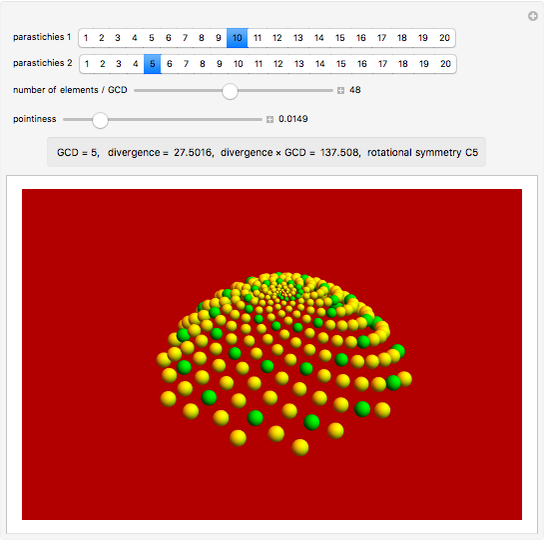
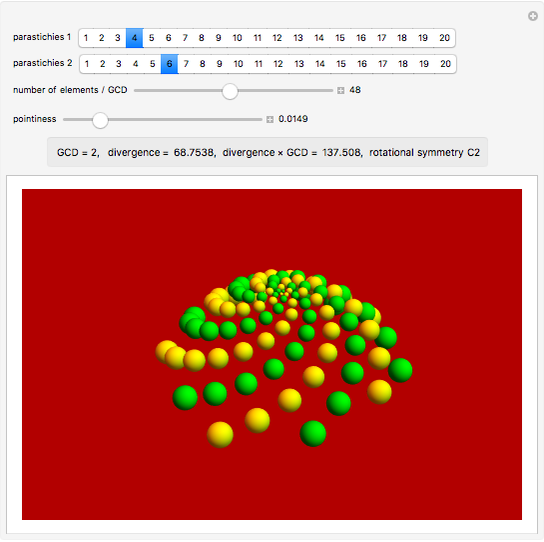
Jean's fundamental theorem of phyllotaxis describes the relationship between the numbers of observed spirals in cylindrical lattices and the horizontal angle between successive vertical spots in the lattice.
[more]
Contributed by: Dmitry Weise (June 2013)
Open content licensed under CC BY-NC-SA
Snapshots
Details
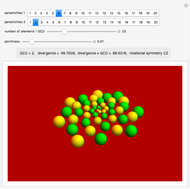
The parastichies are the series of leaves that most readily catch the eye. The number of parastichies rises from the center to the periphery, following a Fibonacci sequence.
GCD is the greatest common divisor.
Divergence angle is the angle between two consecutive leaves.
References
[1] R. V. Jean, Phyllotaxis: A Systemic Study in Plant Morphogenesis, New York: Cambridge University Press, 2009.
[2] D. Weise. "Principle of Minimax and Rise Phyllotaxis (Mechanistic Phyllotaxis Model)." (Jun 6, 2013) www.mi.sanu.ac.rs/vismath/dima.
Permanent Citation
Phyllotaxis Spirals
Stephen Wolfram
Phyllotaxis Spirals in 3D
Stephen Wolfram
Shell Parameter Space
Jayna Resman, Michelle Winerip, Elizabeth Cowdery, and Allison Reed-Harris
Shell Space: The 'Snugness' Condition
Phil Ramsden
Shell Space: Flare, Verm, and Spire
Phil Ramsden
Model of Shell Growth
Stephen Wolfram
Snowflake Growth
Matthew Szudzik
Growth Model for the Blue-Green Alga Anabaena catenula
Enrique Zeleny
Horn Growth in 2D
Stephen Wolfram
Elementary Cellular Automaton Egg
Michael Schreiber
