One-Half the Apothem Times the Perimeter

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
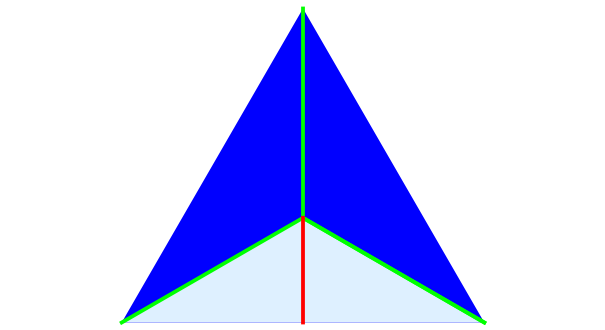
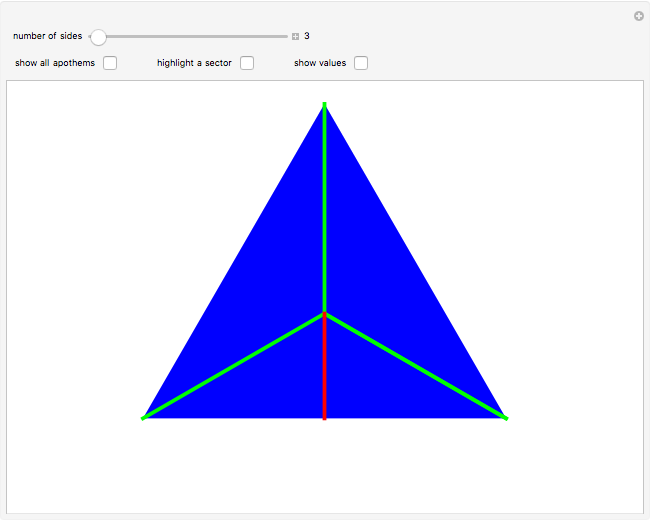
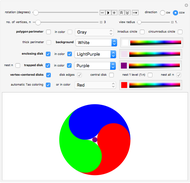
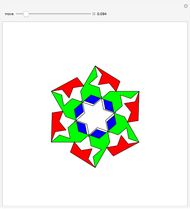
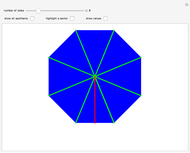
An apothem of a regular polygon is the length of the segment from the center to the midpoint of a side. The area of a regular polygon can be calculated as one-half the apothem multiplied by the perimeter. This Demonstration explains why that formula works.
Contributed by: Daniel Tokarz (July 2016)
Open content licensed under CC BY-NC-SA
Snapshots
Details
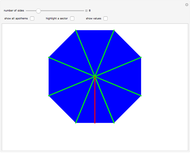
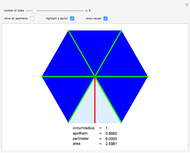
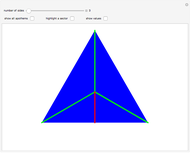
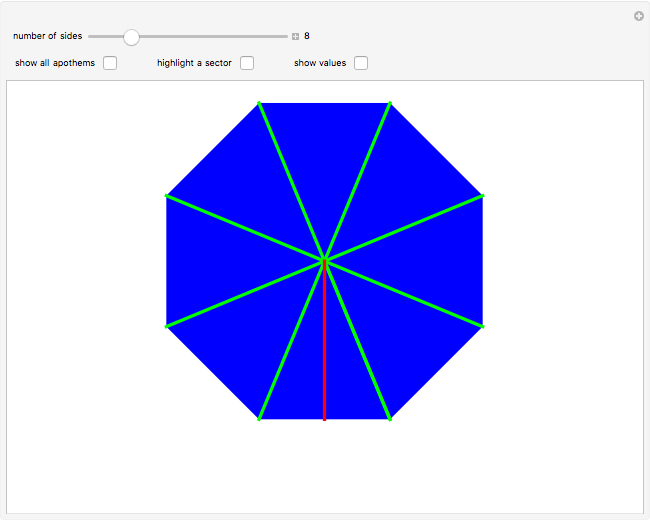
Snapshot 1: each triangle is identical, bounded on the sides by the green circumradii
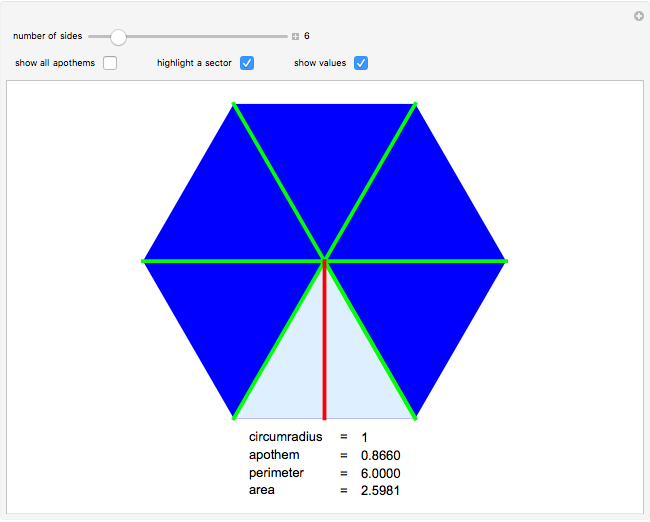
Snapshot 2: the area is equal to 1/2 the area multiplied by the perimeter
Snapshot 3: for as few or as many sides as an  -gon has, this formula works
-gon has, this formula works
Imagine a regular  -sided polygon divided into a set of
-sided polygon divided into a set of  identical isosceles triangles. One such triangle is the sector shown in light blue in the Demonstration. Each triangle has a base of side length
identical isosceles triangles. One such triangle is the sector shown in light blue in the Demonstration. Each triangle has a base of side length  and a height
and a height  equal to the apothem. Thus the area of each triangle is
equal to the apothem. Thus the area of each triangle is 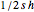 . If we add up all the triangle areas, the area of the entire polygon can be written as
. If we add up all the triangle areas, the area of the entire polygon can be written as 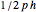 , where
, where 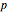 is the perimeter. As
is the perimeter. As 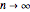 , the polygon approaches a circle. An apothem equals the radius
, the polygon approaches a circle. An apothem equals the radius  , while the perimeter equals
, while the perimeter equals 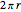 , giving the well-known result for the area of a circle:
, giving the well-known result for the area of a circle: 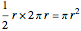 .
.
Permanent Citation