One-Wheeled Robot-Gyrostat

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
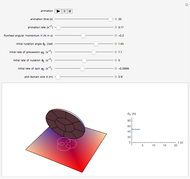
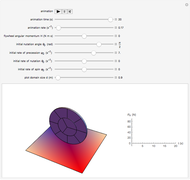
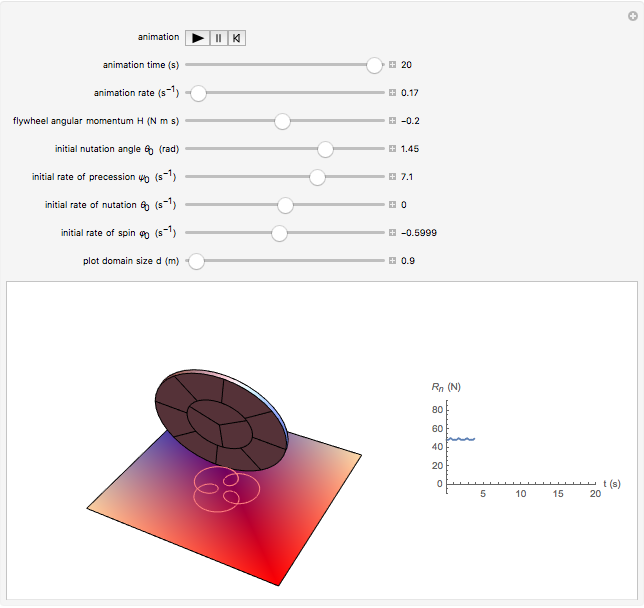
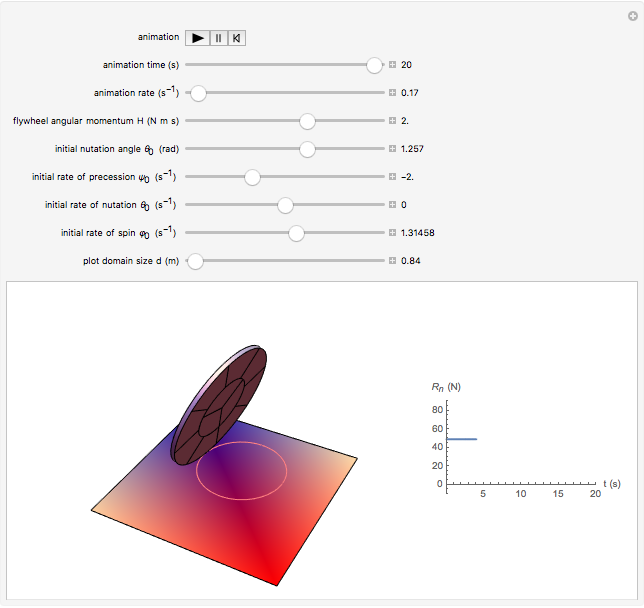
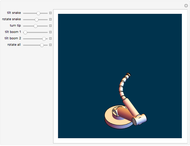
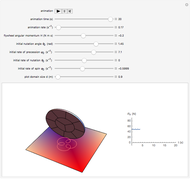
A one-wheeled robot is modeled by a gyrostat consisting of a heavy disk with a balanced rotating flywheel. The disk rolls without sliding on a fixed absolutely rough plane. One can see the different regimes of uncontrolled robotic motion by changing the flywheel angular momentum  and the initial conditions of motion. The trajectory of the contact point and the plot of the plane normal reaction
and the initial conditions of motion. The trajectory of the contact point and the plot of the plane normal reaction  at the contact point are shown. The steady motions are presented in the bookmarks. Negative vertical reaction means that the solution of the equations of motion is not physically realizable.
at the contact point are shown. The steady motions are presented in the bookmarks. Negative vertical reaction means that the solution of the equations of motion is not physically realizable.
Contributed by: Olga Kapustina (MSUAB) and Yuri Martynenko (Lomonosov MSU) (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Steady uncontrolled robot motion can be the basiс dynamics of control modes [1–4]. In [3], the families of steady motion of a robot-gyrostat consisting of a disk with a rotating flywheel were found and conditions for their stability were obtained. This Demonstration is based on the program published in [4]. The numerical parameters of the program's example correspond to a one-wheeled robot [1, 2] developed at the Institute of Mechanics of the Lomonosov Moscow State University. The animation of the robot in the form of a disk without a flywheel can be obtained as a particular case from the program [4].
Snapshot 1: an arbitrary motion of the disk with flywheel
Snapshot 2: the steady motion in which the disk spins about a vertical diameter and the flywheel does not rotate relative to the disk
Snapshot 3: the steady motion in which the contact point of the disk with the plane moves in a circle
Snapshot 4: the steady motion in which the contact point of the disk with the plane moves in a straight line.
Snapshot 5: the steady motion in which the nutation angle  is constant; the disk rotates around the fixed vertical axis at a permanent velocity
is constant; the disk rotates around the fixed vertical axis at a permanent velocity 
Snapshot 6: the physically nonrealizable motion of a disk with flywheel
[1] Y. G. Martynenko, A. V. Lenskii, A. I. Kobrin, "Decomposition of the Problem of Controlling a Mobile One-Wheel Robot with an Unperturbed Gyrostabilized Platform," Doklady Physics, 47(10), 2002 pp. 772–774.
[2] Y. G. Martynenko, "Motion Control of Mobile Wheeled Robots," Journal of Mathematical Science, 147(2), 2007 pp. 6569–6606.
[3] Y. G. Martynenko, "Stability of Uncontrolled Motions of the One-Wheeled Mobile Robot with Flywheel Stabilization System," in Proceedings of the International Conference on Problems of Mechanics of Modern Machines, Vol. 1, Ulan-Ude, Russia, 2000 pp. 96–101 (in Russian).
[4] O. M. Kapustina and Y. G. Martynenko, "Using Animation TechnologyMathematica6 in the Theoretical Mechanics Tasks," in Proceedings of the 3rd International Scientific-Practical Conference on Modern Information Technology and IT Education, Moscow, 2008 pp. 429–436 (in Russian).
Permanent Citation