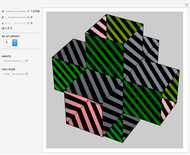
Op Art with an Open, Flexible Four-Cube

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
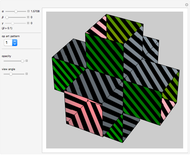
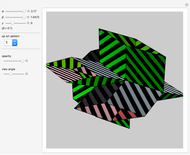
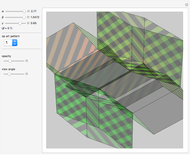
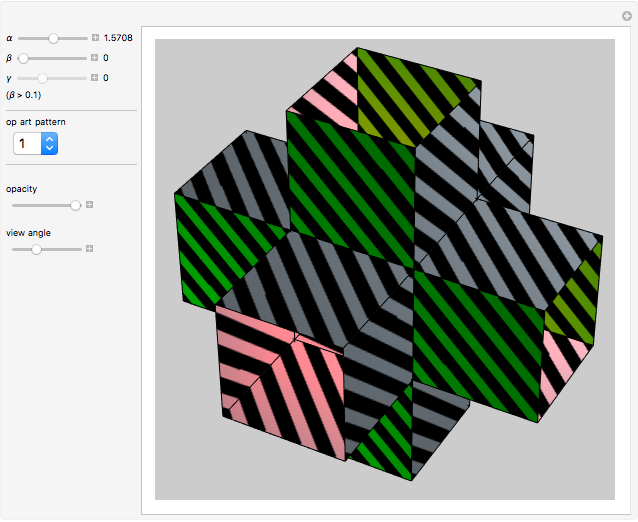
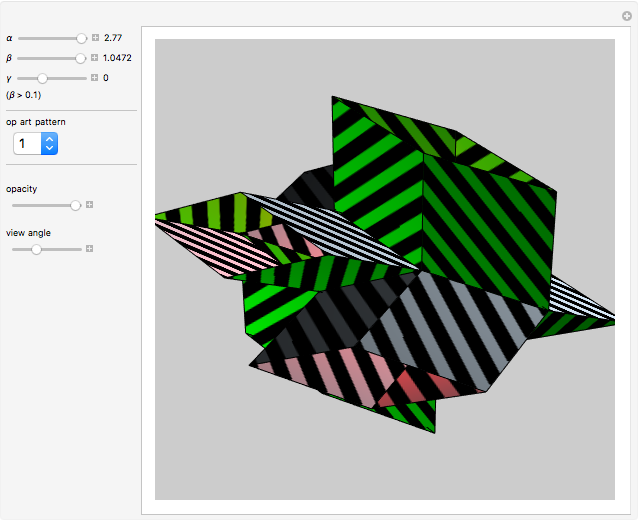
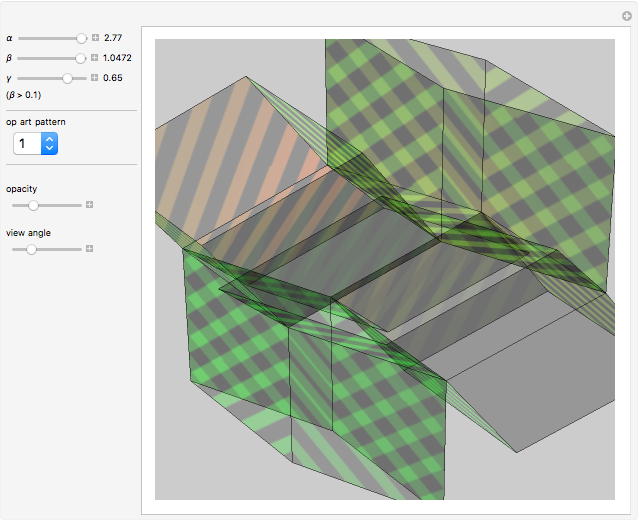
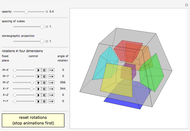
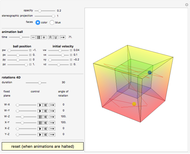
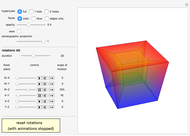
This Demonstration shows an open view of an orthogonal projection for a flexible symmetric four-cube (tesseract) using Slavik Jablan's op art ornaments.
Contributed by: Izidor Hafner and Andjelka Simic (October 2016)
Open content licensed under CC BY-NC-SA
Snapshots
Details
To gain some intuition for the four-cube, consider the sequence where each figure is the extrusion of the previous one in the next dimension: 0D: point, 1D: line, 2D: square, 3D: cube and 4D: hypercube with 1, 2, 4, 8 and 16 vertices. A  -dimensional polytope is bounded by cells of dimension
-dimensional polytope is bounded by cells of dimension  : a square is bounded by four edges, a cube by six squares and a four-cube by eight cubes.
: a square is bounded by four edges, a cube by six squares and a four-cube by eight cubes.
In this Demonstration one of the cubic cells of the four-cube is left out.
Victor Vasarely, the originator of op art in the twentieth century, made transparent sculptures similar to the figures shown here. Jablan Slavik constructed op art transparent four-cubes using black and white squares with a circular arc as a basic element.
References
[1] S. V. Jablan. "Modularity in Art." (Oct 12, 2016) www.mi.sanu.ac.rs/~jablans/d3.htm.
[2] Visual Mathematics. (Oct 12, 2016) www.mi.sanu.ac.rs/vismath.
[3] V. Panfilov. Unwrapping a Tesseract (4d Cube aka Hypercube) [Video]. (Oct 12, 2016) www.youtube.com/watch?v=BVo2igbFSPE.
[4] The Bridges Organization. "Anđelka Simić." Transparent Hypercube (jewelry). (Oct 12, 2016) gallery.bridgesmathart.org/exhibitions/2016-joint-mathematics-meetings/andjelkasimic.
Permanent Citation