Open and Closed Kaleidoscopes

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
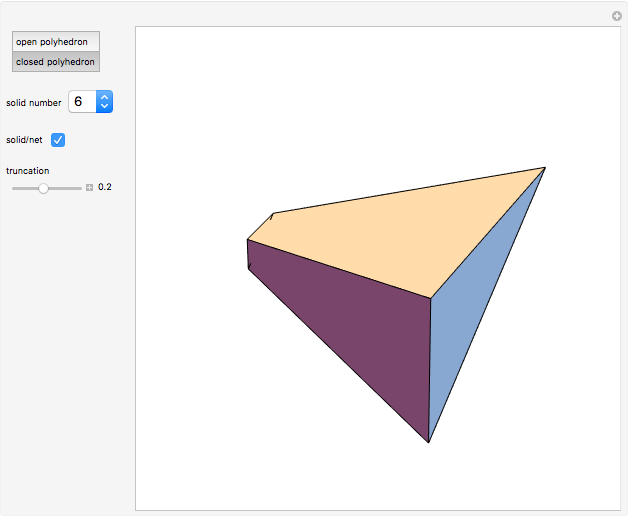
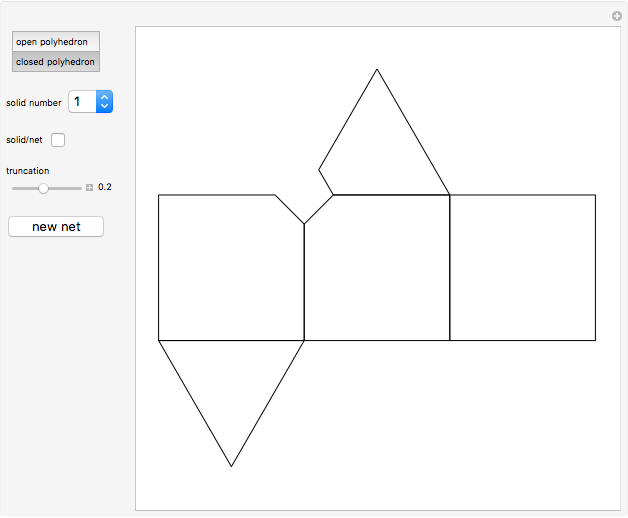
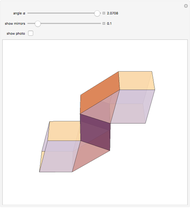
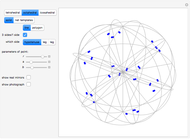
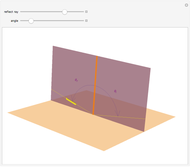
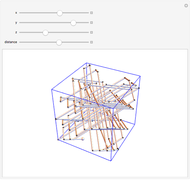
This Demonstration shows two types of kaleidoscopes. The first set consists of four kaleidoscopes based on "open" prismatic polyhedra, without a base or top. The second set consists of prisms and tetrahedra. Nets of polyhedra are shown so that you can build kaleidoscopes using metallic reflecting foil. Since the foil is inside the polyhedron, there is a viewing hole formed as the truncation of one vertex of the original polyhedron.
Contributed by: Izidor Hafner (August 2016)
Open content licensed under CC BY-NC-SA
Snapshots
Details
This Demonstration describes all kaleidoscopes from [1, pp. 155–161] that are not covered in our previous Demonstrations.
The kaleidoscopes based on open triangular prisms have triangular horizontal cross sections with angles  ,
, 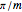 ,
,  , where
, where 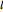 ,
, 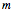 ,
,  are positive integers. The solutions of the equation
are positive integers. The solutions of the equation 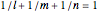 are
are 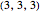 ,
,  ,
, 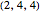 . Varying a point in the triangle gives the vertices of certain isogonal tessellations [1, p. 157].
. Varying a point in the triangle gives the vertices of certain isogonal tessellations [1, p. 157].
Tetrahedral kaleidoscopes are constructed as certain cross sections of a rectangular block of dimensions  [1, p. 159].
[1, p. 159].
Five mirrors can be arranged in the form of certain triangular prisms and lead to solid tessellations of prisms [1, p. 160].
Six mirrors are arranged as the sides of a rectangular prism to give a solid tessellation of rectangular blocks [1, p. 161].
Reference
[1] W. W. R. Ball and H. S. M. Coxeter, Mathematical Recreations and Essays, 13th ed., New York: Dover Publications, 1987.
Permanent Citation