Optical Pumping: Population Dynamics

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
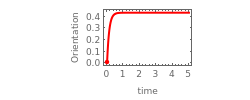
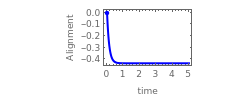
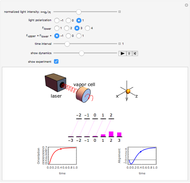
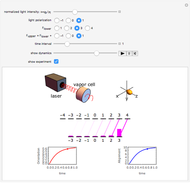
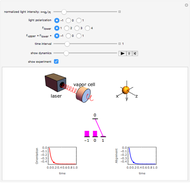
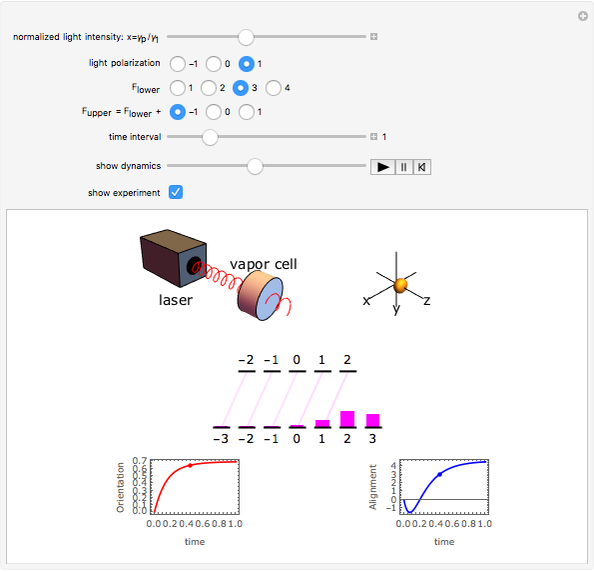
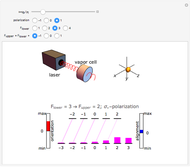
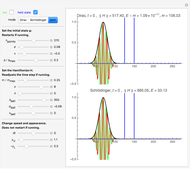
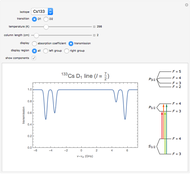
This module illustrates the dynamical, i.e., time‐dependent, rearrangement of Zeeman sublevel populations by optical pumping of atoms with circularly or linearly polarized light. The power and polarization of the light as well as the angular momenta of the states coupled by the light can be chosen. The effect of optical pumping is illustrated by the relative sublevel populations, by the two lowest multipole moments (orientation and alignment), and by a probability surface. The length of the displayed time interval can be chosen and the dynamics of the populations, the orientation (vector polarization) and the alignment (tensor polarization) of the atomic medium can be seen as animations.
Contributed by: Antoine Weis (Université de Fribourg) and Gianni Di Domenico (Université de Neuchâtel) (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
When an atomic medium is irradiated with (circularly or linearly) polarized light that is resonant with a transition between states of angular momenta 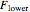 and
and  the medium becomes spin polarized. The origin of this polarization is a transfer of populations
the medium becomes spin polarized. The origin of this polarization is a transfer of populations  between the magnetic sublevels
between the magnetic sublevels  by subsequent cycles of light absorption and emission. In this module, the dynamics of the optical pumping process is addressed by showing the time dependence of the
by subsequent cycles of light absorption and emission. In this module, the dynamics of the optical pumping process is addressed by showing the time dependence of the  populations
populations  obtained by solving rate equations. Upward transitions are driven at a rate
obtained by solving rate equations. Upward transitions are driven at a rate 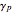 , and allowance for sublevel relaxation at a rate
, and allowance for sublevel relaxation at a rate 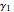 is made, so that the optical pumping can be parametrized in terms of a dimensionless variable
is made, so that the optical pumping can be parametrized in terms of a dimensionless variable 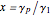 that is proportional to the light intensity.
that is proportional to the light intensity.
The light polarization can be chosen as  (linear polarization) or
(linear polarization) or  (left-/right-handed circular polarization) which implies the selection rules
(left-/right-handed circular polarization) which implies the selection rules 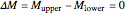 , and ±1, respectively. The transitions between sublevels are shown by vertical (or skewed) lines whose intensity is proportional to the product of the sublevel population and the relative transition strength (itself proportional to a squared 3j-symbol). In this way one sees how the absorbed (and hence also the reemitted) light intensity changes as the pumping proceeds.
, and ±1, respectively. The transitions between sublevels are shown by vertical (or skewed) lines whose intensity is proportional to the product of the sublevel population and the relative transition strength (itself proportional to a squared 3j-symbol). In this way one sees how the absorbed (and hence also the reemitted) light intensity changes as the pumping proceeds.
Sublevel populations are represented by vertical bars.
Depending on the relative sublevel populations, the polarized medium may either absorb less light than the unpolarized medium (dark state) or more light than the unpolarized medium (bright state). The former case occurs in 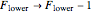 and
and 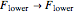 transitions, while the latter case is encountered in
transitions, while the latter case is encountered in  transitions (both with linear and circularly polarized light).
transitions (both with linear and circularly polarized light).
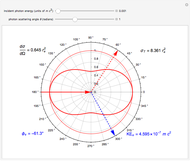
In thermal equilibrium, i.e., in the absence of light, all levels have an identical population of 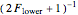 . Optical pumping leads to a non-equilibrium population distribution and the medium is said to be polarized. The polarization of a medium can be defined in terms of its longitudinal multipole moments
. Optical pumping leads to a non-equilibrium population distribution and the medium is said to be polarized. The polarization of a medium can be defined in terms of its longitudinal multipole moments  (see also Polarized Atoms Visualized by Multipole Moments). The only longitudinal multipole moments to which light on an electric dipole transition couples are the orientation
(see also Polarized Atoms Visualized by Multipole Moments). The only longitudinal multipole moments to which light on an electric dipole transition couples are the orientation  and the alignment
and the alignment 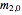 which can be defined in terms of the sublevel populations
which can be defined in terms of the sublevel populations  as
as
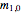 ∝
∝ 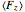 =
= 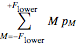 , for the orientation, and
, for the orientation, and
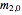 ∝
∝ 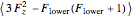 =
= 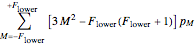 , for the alignment.
, for the alignment.
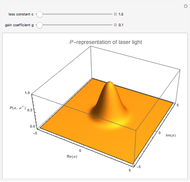
The state of polarization can also be represented in terms of a probability surface 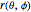 , which represents the probability to find the system in the state
, which represents the probability to find the system in the state 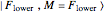 , when making a measurement with the quantization axis oriented along the spherical direction given by (
, when making a measurement with the quantization axis oriented along the spherical direction given by ( ,
,  ). In thermal equilibrium (
). In thermal equilibrium ( ) this surface is a sphere of radius
) this surface is a sphere of radius 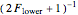 . Note that the probability surface reflects the (rotational and reflection) symmetry of the light polarization. For states with a pure longitudinal polarization (no coherences) the probability surface has a rotational symmetry around the
. Note that the probability surface reflects the (rotational and reflection) symmetry of the light polarization. For states with a pure longitudinal polarization (no coherences) the probability surface has a rotational symmetry around the  axis and can be expressed in terms of the sublevel populations
axis and can be expressed in terms of the sublevel populations  and specific matrix elements of the Wigner rotation matrices
and specific matrix elements of the Wigner rotation matrices 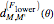 as
as
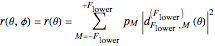 .
.
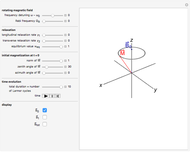
Note also that for pumping with circularly polarized light the quantization axis ( axis) is oriented along the direction of light propagation, while for pumping with linearly polarized light the quantization axis is along the direction of oscillation of the optical field.
axis) is oriented along the direction of light propagation, while for pumping with linearly polarized light the quantization axis is along the direction of oscillation of the optical field.
Permanent Citation