Optical Rogue Waves (Rogons)

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
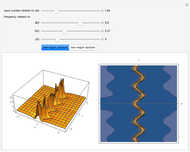
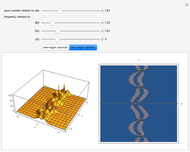
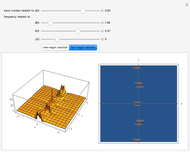
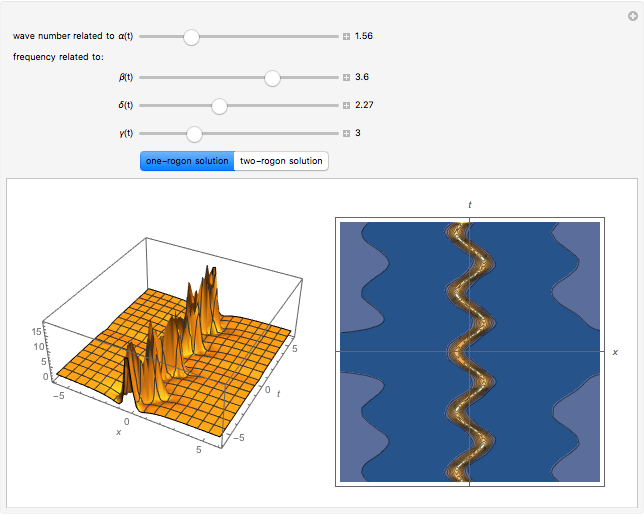
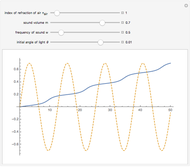
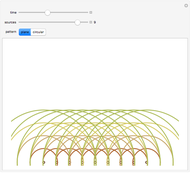
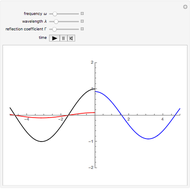
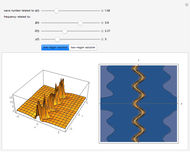
This Demonstration plots the dynamical behavior of one-rogon (rogue wave) and two-rogon solutions are plotted for the inhomogeneous nonlinear Schrödinger (NLS) equation with variable coefficients  . Some particular functions of time are chosen to exhibit the solutions.
. Some particular functions of time are chosen to exhibit the solutions.
Contributed by: Zhenya Yan (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Rogue waves (or RWs or rogons) are also known as freak waves, monster waves, killer waves, giant waves, huge waves, super waves, gigantic waves, or extreme waves, etc. They occur in many fields, such as oceanography, optical fibers, etc. Many news media have recently reported the RW phenomenon, including Nature News, BBC News, PhysOrg, Reuters, Science Daily, Physics World, Physics.org, The Financial Express, Scientific American, etc.
The explicit rogue solution of the NLS equation was first derived in [1] (the solution was called the Peregrine breather or algebraic breather). Optical rogue waves have been observed in optical fibers [2]. A direct approach to find multi-rogon solutions of the NLS equation based on the modified Darboux transformation was presented in [3].
The term rogon was also coined for a rogue wave and rogon-like solutions were shown for the inhomogeneous NLS equation with variable coefficients. This entails some choices for functions of time in the Demonstration. Periodic and hyperbolic wave functions exhibited the dynamical behavior of rogue-like wave phenomenon. Here, four parameters control the rogue wave propagation. For more details on one-rogon (rogue wave) and two-rogon solutions of the inhomogeneous NLS equation with variable coefficients, see [4].
[1] D. H. Peregrine, "Water Waves, Nonlinear Schrödinger Equations and Their Solutions," J. Austral. Math. Soc. Ser. B, 25, 1983 pp. 16–43.
[2] D. R. Solli, C. Ropers, P. Koonath, and B. Jalali, "Optical Rogue Waves," Nature, 450, 2007 pp. 1054–1057.
[3] N. Akhmediev, A. Ankiewicz, and M. Taki, "Waves That Appear from Nowhere and Disappear without a Trace," Phys. Lett. A, 373(6), 2009 pp. 675–678; N. Akhmediev, A. Ankiewicz, and J. M. Soto-Crespo, "Rogue Waves and Rational Solutions of the Nonlinear Schrödinger Equation," Phys. Rev. E, 80(2), 2009.
[4] Z. Yan, "Financial Rogue Waves," Phys. Lett. A, 2009.
Permanent Citation
"Optical Rogue Waves (Rogons)"
http://demonstrations.wolfram.com/OpticalRogueWavesRogons/
Wolfram Demonstrations Project
Published: March 7 2011