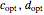Optimal Joint Measurements of Qubit Observables

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
In quantum mechanics, two incompatible sharp observables 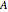 and
and 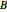 can nevertheless be simultaneously approximated by noisy measurements
can nevertheless be simultaneously approximated by noisy measurements  and
and 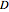 at the expense of tolerating some inaccuracy. By quantifying this inaccuracy using a measure of error denoted here by
at the expense of tolerating some inaccuracy. By quantifying this inaccuracy using a measure of error denoted here by  , we want to find the pair
, we want to find the pair 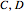 that most accurately approximates
that most accurately approximates  under the constraint of joint measurability, and in doing so characterize the lower bound of the admissible region of error pairs spanned by all pairs of compatible approximators.
under the constraint of joint measurability, and in doing so characterize the lower bound of the admissible region of error pairs spanned by all pairs of compatible approximators.
Contributed by: Tom Bullock and Paul Busch (January 2017)
(Department of Mathematics, University of York, York, UK)
Open content licensed under CC BY-NC-SA
Snapshots
Details
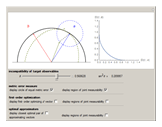
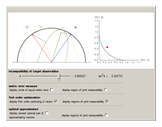
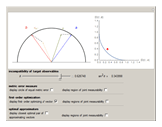
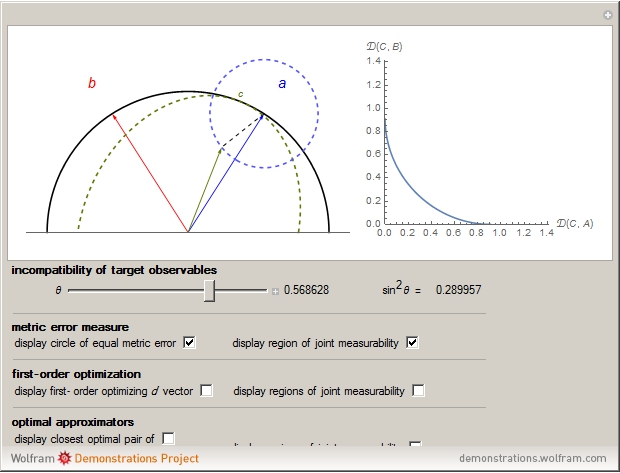
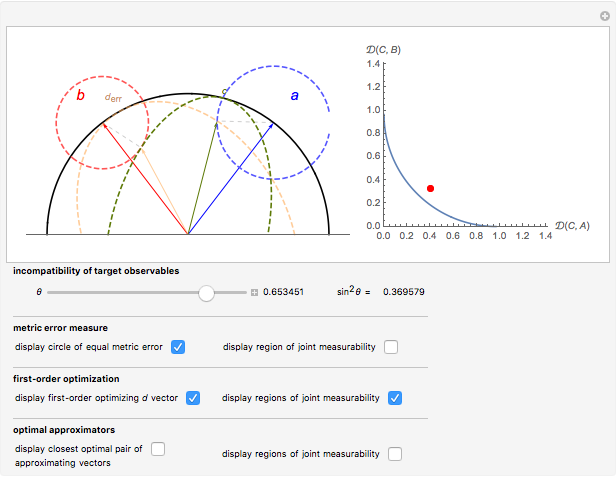
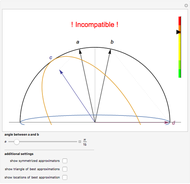
This Demonstration considers a one-qubit system. Assume that the observables in question are dichotomic (two-valued) and unbiased; such an observable  is expressed as the set of positive operators (commonly referred to as a POVM)
is expressed as the set of positive operators (commonly referred to as a POVM) 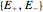 where
where 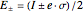 , with Bloch vector
, with Bloch vector  ,
, 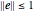 , and
, and  is a vector whose elements are the three Pauli matrices. This is the Bloch vector plotted in this Demonstration. The incompatible observables
is a vector whose elements are the three Pauli matrices. This is the Bloch vector plotted in this Demonstration. The incompatible observables  have normalized Bloch vectors
have normalized Bloch vectors 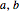 , with associated Hermitian operators
, with associated Hermitian operators  ,
,  , and the degree of incompatibility between
, and the degree of incompatibility between  is given by
is given by 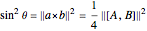 , where
, where  denotes the operator norm. The approximating observables
denotes the operator norm. The approximating observables  and
and 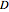 are described in terms of the (generally subnormalized) Bloch vectors
are described in terms of the (generally subnormalized) Bloch vectors  and
and  , respectively. It is known that for these observables to be jointly measurable, it is necessary and sufficient that they satisfy
, respectively. It is known that for these observables to be jointly measurable, it is necessary and sufficient that they satisfy 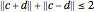 . If we fix
. If we fix  , for instance, then we define an ellipsoid
, for instance, then we define an ellipsoid 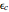 of joint measurability with respect to
of joint measurability with respect to  :
:
 ,
,
and similarly we can define the ellipsoid 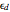 for observables
for observables  jointly measurable with
jointly measurable with 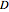 . It can be shown that the optimal approximators lie within the plane spanned by
. It can be shown that the optimal approximators lie within the plane spanned by  and
and  [1], and so we restrict to this circle within the Bloch sphere, and
[1], and so we restrict to this circle within the Bloch sphere, and  reduce to ellipses inscribed in this circle. As can be seen, by moving the location of
reduce to ellipses inscribed in this circle. As can be seen, by moving the location of  , the shape of the ellipse changes: it will be near a line along
, the shape of the ellipse changes: it will be near a line along  as
as  nears the surface of the circle, and it approaches a circle as
nears the surface of the circle, and it approaches a circle as  nears the origin. The measure of error
nears the origin. The measure of error  used is given by the metric of Bloch vectors in the qubit case (for a generic physical interpretation in terms of differences of the associated probability distributions, see [1, 2]),
used is given by the metric of Bloch vectors in the qubit case (for a generic physical interpretation in terms of differences of the associated probability distributions, see [1, 2]),
 .
.
Geometrically, the Bloch vectors associated with observables  of constant error relative to
of constant error relative to 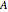 lie in a circle around the endpoint of
lie in a circle around the endpoint of  , and so, while moving around this circle we are able to keep
, and so, while moving around this circle we are able to keep 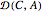 fixed, all the while changing the ellipse of joint measurability, allowing us to find different observables
fixed, all the while changing the ellipse of joint measurability, allowing us to find different observables 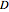 that minimize the error
that minimize the error 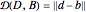 . Assuming that we fix
. Assuming that we fix  , by minimizing the error
, by minimizing the error  under the constraint of joint measurability we find that the minimizing vector
under the constraint of joint measurability we find that the minimizing vector  must lie on the edge of the ellipse
must lie on the edge of the ellipse 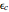 ; that is,
; that is, 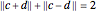 , and the circle of radius
, and the circle of radius  centered at
centered at  must be tangent to
must be tangent to 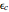 at
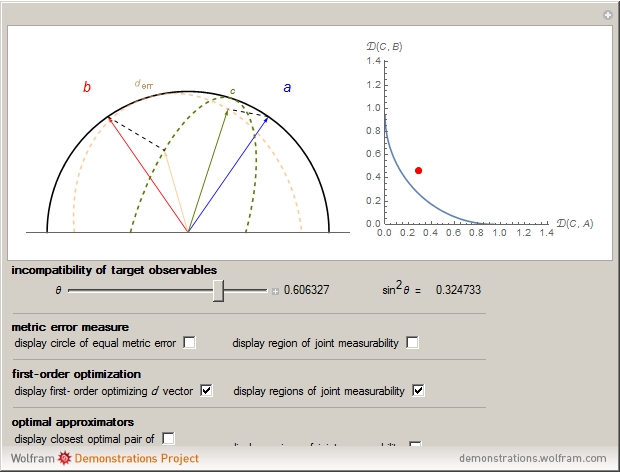
at  . This is demonstrated by choosing the first-order optimization, where the
. This is demonstrated by choosing the first-order optimization, where the  vector with the smallest associated error is found under the constraint of joint measurability. An optimal pair of approximating observables will be such that their associated Bloch vectors will lie on the surface of their respective joint measurability ellipses, and these ellipses will be tangent to the fixed error circles at that point. This is demonstrated by choosing the optimal approximators option, which finds the closest pair of observables that minimize the pair of errors.
vector with the smallest associated error is found under the constraint of joint measurability. An optimal pair of approximating observables will be such that their associated Bloch vectors will lie on the surface of their respective joint measurability ellipses, and these ellipses will be tangent to the fixed error circles at that point. This is demonstrated by choosing the optimal approximators option, which finds the closest pair of observables that minimize the pair of errors.
As originally proven in [3], the minimum error curve in the plot is given parametrically, with 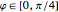 :
:
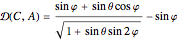 ,
,
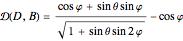 .
.
It is shown in [4] that this boundary curve of the admissible error region reflects a tradeoff between the two approximation errors and the degrees of the unsharpness of the approximating observables 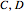 that is governed by the degree of incompatibility of the target observables
that is governed by the degree of incompatibility of the target observables  .
.
References
[1] P. Busch and T. Heinosaari, "Approximate Joint Measurements of Qubit Observables," Quantum Information and Computation, 8(8), 2008 pp. 797–818.
[2] P. Busch, P. Lahti and R. F. Werner, "Heisenburg Uncertainty for Qubit Measurements," Physical Review A, 89(1), 2014 012129. doi:10.1103/PhysRevA.89.012129.
[3] S. Yu and C. H. Oh, "Optimal Joint Measurement of Two Observables of a Qubit." arxiv.org/abs/1402.3785.
[4] T. Bullock and P. Busch, "Measurement Uncertainty: The Problem of Characterising Optimal Error Bounds." arxiv.org/abs/1512.00104.
Permanent Citation