Wolfram Demonstrations Project

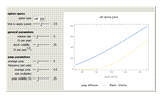
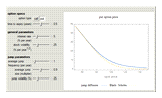
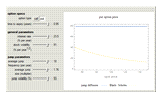
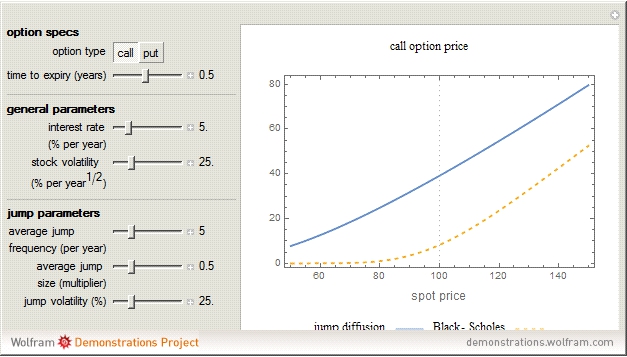
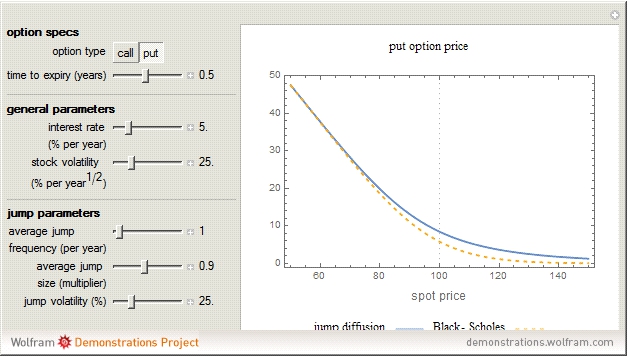
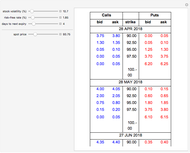
The jump diffusion model, introduced in 1976 by Robert Merton, is a model for stock price behavior that incorporates small day-to-day "diffusive" movements together with larger, randomly occurring "jumps". The inclusion of jumps allows for more realistic "crash" scenarios and means that the standard dynamic replication hedging approach of the standard Black-Scholes model no longer works. This causes option prices to increase compared to the Black-Scholes model and to depend on the risk aversion of investors. This Demonstration explores how the price of European call and put options varies with the jump diffusion model parameters.

Contributed by: Peter Falloon

In the jump diffusion model, the stock price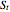

follows the random process

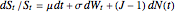. The first two terms are familiar from the Black-Scholes model: drift rate

, volatility

, and random walk (Wiener process)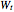

. The last term represents the jumps:

is the jump size as a multiple of stock price while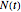

is the number of jump events that have occurred up to time

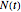is assumed to follow the Poisson process

, where

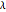is the average number of jumps per unit time. The jump size may follow any distribution, but a common choice is a log-normal distribution

, where

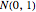is the standard normal distribution,

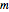is the average jump size, and

is the volatility of jump size. The three parameters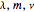

characterize the jump diffusion model.

For European call and put options, closed-form solutions for the price can be found within the jump diffusion model in terms of Black-Scholes prices. If we write

as the Black-Scholes price of a call or put option with spot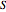

, strike

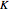, volatility

, interest rate

(assumed constant for simplicity), and time to expiry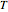

, then the corresponding price within the jump diffusion model can be written as:

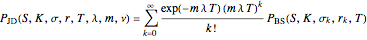where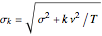

and

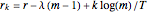. The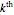

term in this series corresponds to the scenario where

jumps occur during the life of the option.

It can be shown that for all derivatives with convex payoff (which includes regular call and put options) the price always increases when jumps are present (i.e., when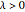

)—regardless of the average jump direction. Thus, holding other parameters constant, the option price is a minimum for

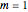(i.e., the Black-Scholes case) and increases both for

and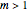

. This increase in price can be interpreted as compensation for the extra risk taken by the option writer due to the presence of jumps, since this risk cannot be eliminated by delta hedging (see Joshi 2003, Section 15.5).