Origami Flanged Pots

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
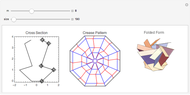
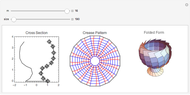
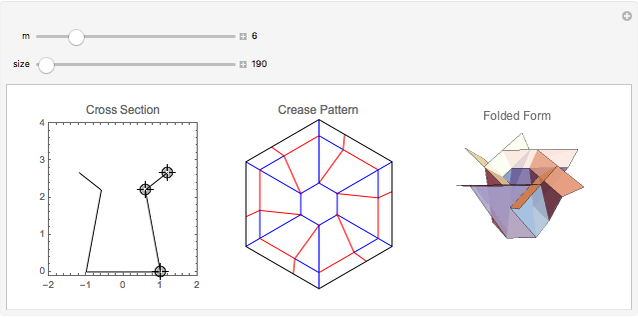
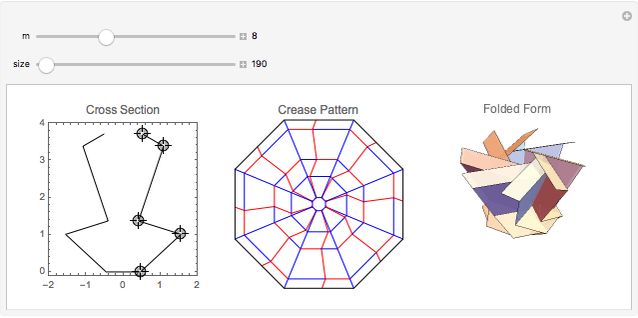
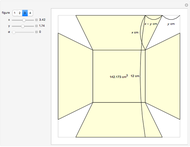
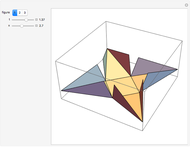
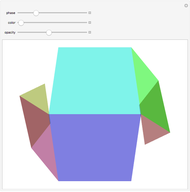
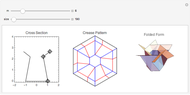
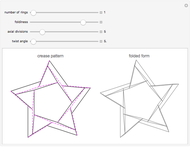
This Demonstration constructs an origami solid of rotation. The left image lets you define the cross section of the desired shape. The middle image is the crease pattern (blue = valley, red = mountain) that folds into a 3D origami shape (right) whose cross section matches what you defined on the left. The sliders control the rotational symmetry and the sizes of the three images.
Contributed by: Robert J. Lang (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
This Demonstration constructs the crease pattern and folded form of a 3D origami solid of rotation, folded from a single uncut 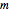 -gon of paper (where
-gon of paper (where 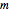 is one of the control values). In the left panel, you manipulate and adjust control points that give the desired cross section. The center panel shows the crease pattern that folds into the desired shape; the right panel shows the 3D folded form of the result.
is one of the control values). In the left panel, you manipulate and adjust control points that give the desired cross section. The center panel shows the crease pattern that folds into the desired shape; the right panel shows the 3D folded form of the result.
You can create any cross section you want by adding and/or moving the locators, but you should keep the locators in the right half of the cross section image and the cross section needs to increase monotonically in height (that is, you can turn the lip inward or outward as you add points, but you can't turn it back toward the ground).
All of the functions necessary to create the tessellation are included in this Demonstration, and the function MakeUniPot is the main function. It takes a list of points that defines the cross section and returns a list {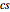 ,
, 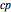 ,
, 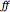 }, where
}, where 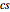 is a list of graphics primitives giving the cross section,
is a list of graphics primitives giving the cross section, 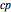 is a list of graphics primitives of the crease pattern, and
is a list of graphics primitives of the crease pattern, and 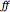 is a list of graphics 3D primitives of the folded form. If you would like to try actually folding one of these tessellations, you can extract the crease pattern from the list returned by MakeUniPot, print it separately, and/or export it to a graphics program for further manipulation.
is a list of graphics 3D primitives of the folded form. If you would like to try actually folding one of these tessellations, you can extract the crease pattern from the list returned by MakeUniPot, print it separately, and/or export it to a graphics program for further manipulation.
This form is an example of the interdisciplinary field of mathematical origami, which has roots in both the traditional art of origami and also in the general analysis of developable surfaces and related forms in mathematics, design, and architecture. This particular shape is based on the simple flat twist from origami tessellations, a field in which pioneering work was done by Shuzo Fujimoto in the latter part of the twentieth century, with significant developments from Chris K. Palmer in the 1990s. Palmer's "polypouches" demonstrated the basic concept I have developed here. The field of mathematical folding is rapidly growing, with new algorithms being developed by many researchers both inside and outside of the traditional origami community.
For examples of what some of these patterns look like in real paper, photographs of several folded examples may be found at Robert J. Lang, Origami.
Permanent Citation