Oscillations of a Mass-Spring System on an Inclined Plane

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
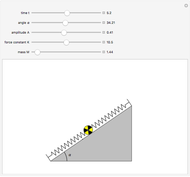
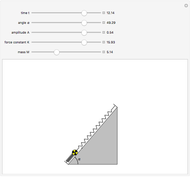
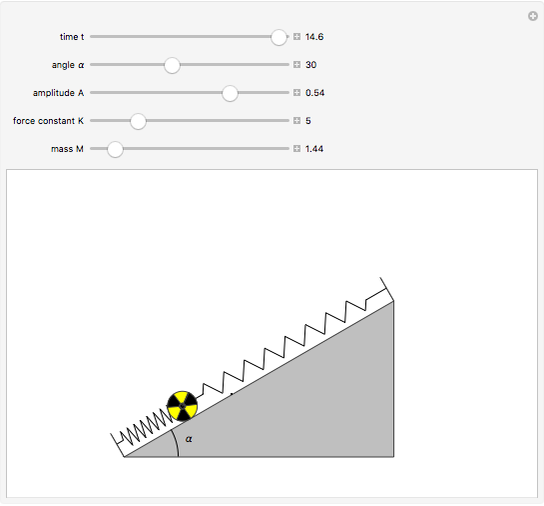
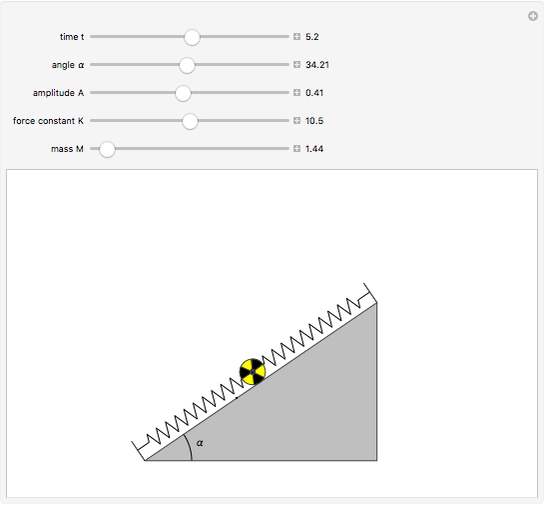
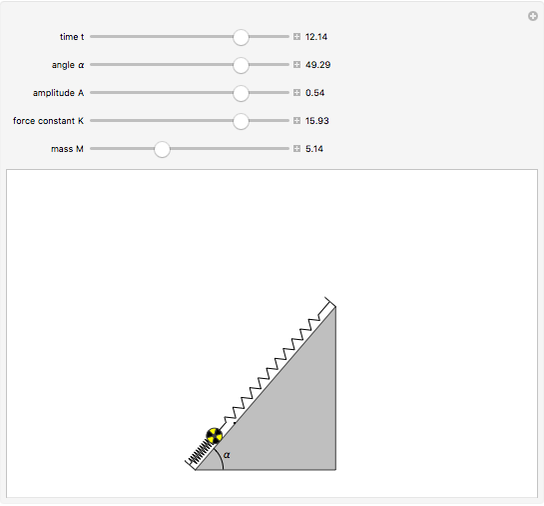
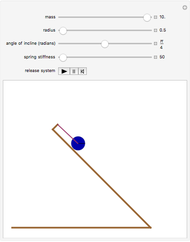
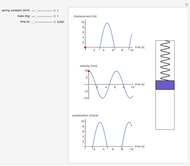
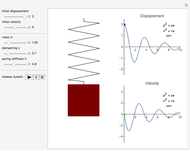
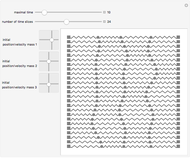
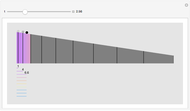
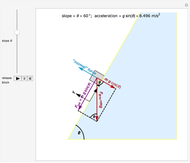
This Demonstration shows the oscillations of a system composed of two identical springs with force constant  attached to a disk of radius
attached to a disk of radius  and mass
and mass 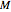 that rolls without sliding on a plane inclined at angle
that rolls without sliding on a plane inclined at angle  . The resultant amplitude is
. The resultant amplitude is 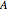 .
.
Contributed by: Edwin Loaiza Acuña (March 2011)
(Universidad del Valle sede Buga. Guadalajara de Buga, Colombia, Sudamérica)
Open content licensed under CC BY-NC-SA
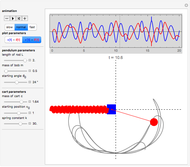
Snapshots
Details
Using Newton's second law, it is possible to establish the equilibrium point 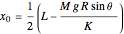 , where
, where 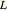 is the length of the incline,
is the length of the incline,  is the acceleration due to gravity, and
is the acceleration due to gravity, and  is a parameter that determines the rotation of the wheel. By energy conservation, one can find the angular frequency:
is a parameter that determines the rotation of the wheel. By energy conservation, one can find the angular frequency:  . From this, the equation of motion for the
. From this, the equation of motion for the  coordinate, measured along the surface, is found to be
coordinate, measured along the surface, is found to be  . The parameters
. The parameters  ,
, 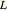 ,
, 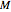 ,
,  , and
, and  all appear in the result.
all appear in the result.
Permanent Citation