Osmotic Pressure

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
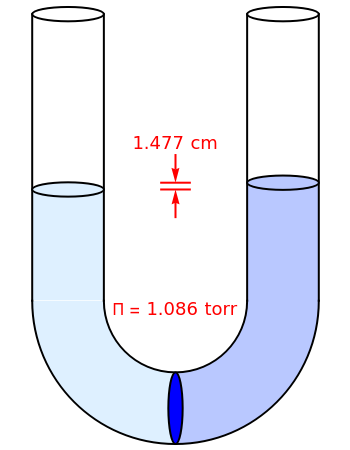
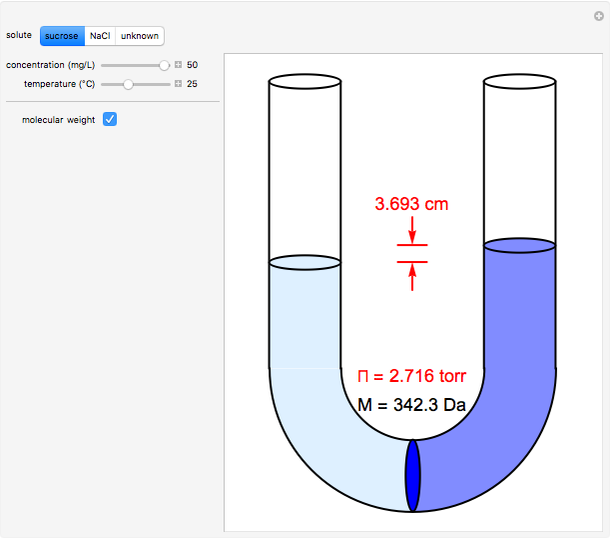
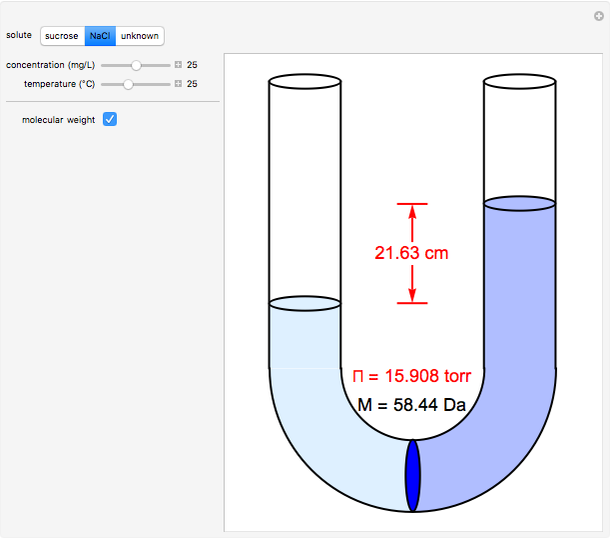
Osmosis involves the selective passage of certain components of a solution through a semipermeable membrane, with exclusion of other components. It is, of course, of central significance in biological processes. Consider in this Demonstration a membrane permeable only to water, but impermeable to the solute in a water solution. The membrane is represented by a blue disk at the bottom of the U-tube, separating the pure solvent on the left from the solution on the right. Solvent will spontaneously flow through the membrane into the solution, in a (vain) attempt to equalize the concentrations on the two sides. This gives rise to an osmotic pressure, designated  . For dilute solutions, the osmotic pressure, in atm, is well approximated by the van 't Hoff equation
. For dilute solutions, the osmotic pressure, in atm, is well approximated by the van 't Hoff equation  , where
, where  is the solute concentration in mol/L,
is the solute concentration in mol/L,  L atm
L atm 
 , the ideal-gas constant, and
, the ideal-gas constant, and  , the absolute temperature in K. The van 't Hoff factor
, the absolute temperature in K. The van 't Hoff factor  represents the number of ions per molecule for a dissociated solute. For example, for NaCl,
represents the number of ions per molecule for a dissociated solute. For example, for NaCl,  , giving the total number of
, giving the total number of  and
and  ions. All other solutes we consider are undissociated with
ions. All other solutes we consider are undissociated with  . The van 't Hoff equation can be written in a form remarkably analogous to the ideal gas law:
. The van 't Hoff equation can be written in a form remarkably analogous to the ideal gas law:  , but the underlying mechanisms for the two phenomena are completely different. Osmotic measurements provide a very sensitive method for determining molecular weights
, but the underlying mechanisms for the two phenomena are completely different. Osmotic measurements provide a very sensitive method for determining molecular weights  , particularly for polymers. For a solute concentration of
, particularly for polymers. For a solute concentration of  g/L, the molar concentration
g/L, the molar concentration  is equal to
is equal to  .
.
Contributed by: S. M. Blinder (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
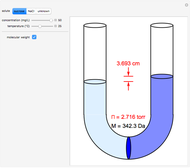
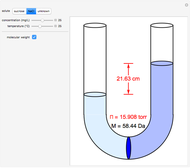
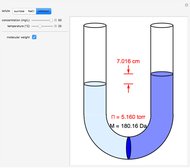
Snapshots 1–3: determining molecular weights for three different solutes
See the Wikipedia entry for Osmotic pressure.
Permanent Citation