Other Formulations of the Collatz Problem

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
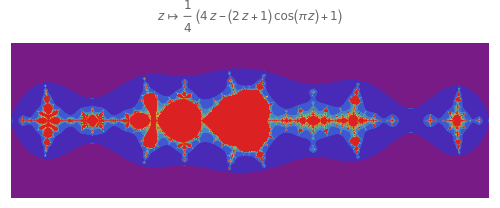
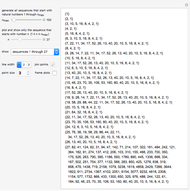
Start with an integer  ; if
; if  is even, divide by 2, but if
is even, divide by 2, but if  is odd, triple it and add 1; repeat this process. The Collatz problem asks whether 1 is reached. In all known cases, the sequence always reaches 1, but no proof is known that this is always true. There are several equivalent formulations of the problem, some generalizations, optimizations, and a variety of properties; some of them are presented here.
is odd, triple it and add 1; repeat this process. The Collatz problem asks whether 1 is reached. In all known cases, the sequence always reaches 1, but no proof is known that this is always true. There are several equivalent formulations of the problem, some generalizations, optimizations, and a variety of properties; some of them are presented here.
Contributed by: Enrique Zeleny (September 2014)
Open content licensed under CC BY-NC-SA
Snapshots
Details
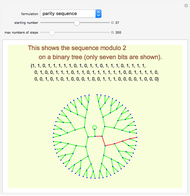
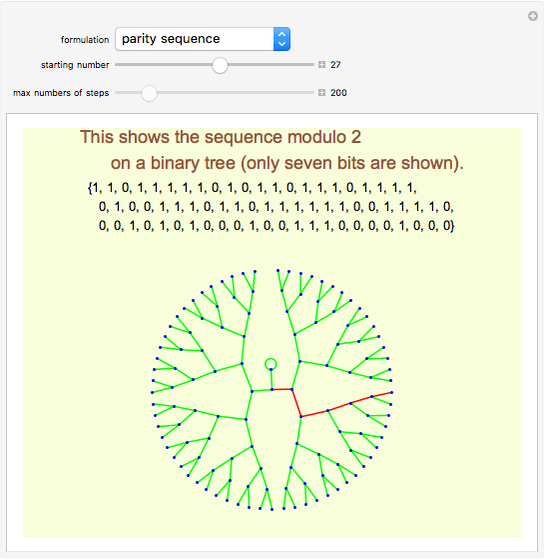
Here is an example using the tag system. Write the number in unary, then remove the first two digits and add the result of applying the rules to the first digit of the previous step; the final result is 1:

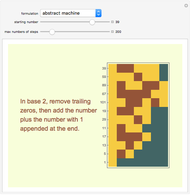
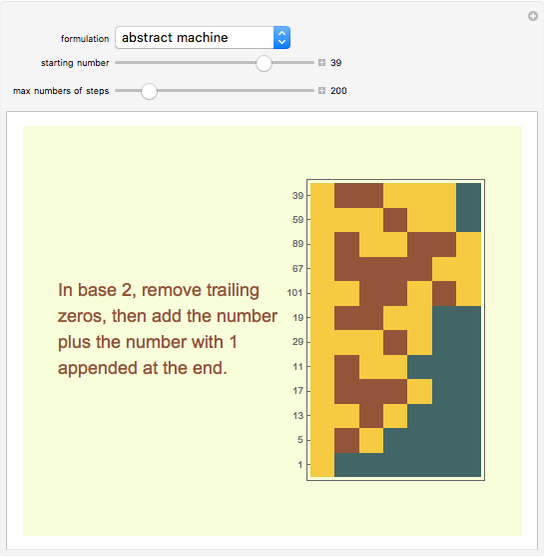
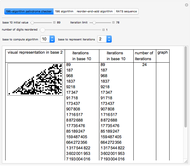
For the abstract machine, notice that an even number in base two ends in zero, like the case of 12, whose digits in binary are {1,1,0,0}. Remove the 0s to get 3 with digits {1,1}, corresponding to halving 12 and 6, then add {1,1} and {1,1,1} (a 1 is appended at the end), equivalent to the operation 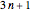 , yielding 10 with digits {1,0,1,0}. Then repeat the operation.
, yielding 10 with digits {1,0,1,0}. Then repeat the operation.

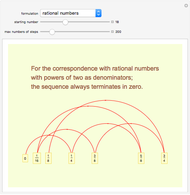
where 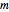 is the denominator and
is the denominator and  the denominator, until the denominator is 0.
the denominator, until the denominator is 0.
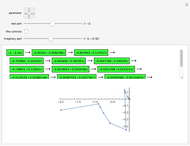
The Syracuse function works with odd integers; start with  and compute
and compute 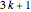 , factor it as the product of a power of 2 and an odd integer
, factor it as the product of a power of 2 and an odd integer 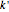 , which is the new term of the sequence; for example
, which is the new term of the sequence; for example 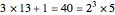 .
.
For more details about the implementation of most of the formulations presented, see the Related Links and [1].
Reference
[1] Wikipedia. "Collatz Conjecture." (Sep 23, 2014) en.wikipedia.org/wiki/Collatz_conjecture.
Permanent Citation