Outer Billiards on Regular Polygons

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
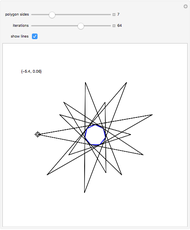
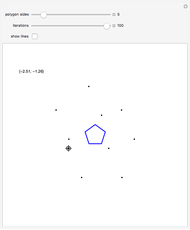
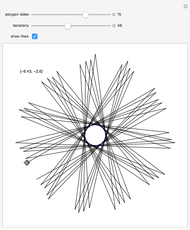
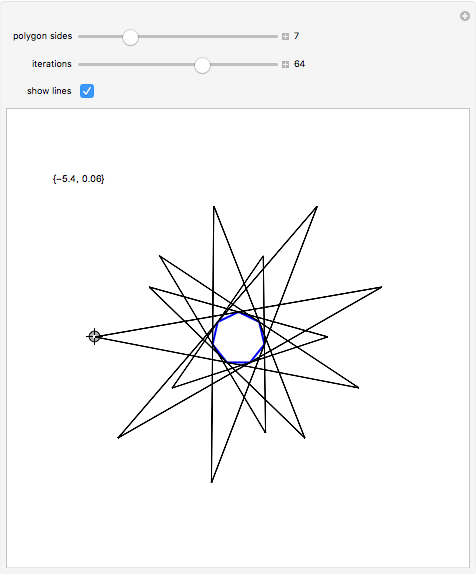
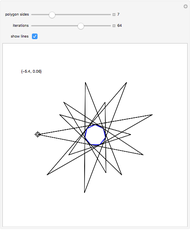
Move the locator to choose a point 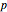 outside a polygon
outside a polygon 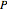 . The outer billiards map
. The outer billiards map  searches clockwise for the nearest vertex
searches clockwise for the nearest vertex  of
of 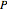 . Let
. Let 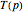 be the reflection of
be the reflection of 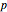 in
in  (i.e.
(i.e. 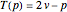 ), a discrete form of orbital dynamics. Iterate this process to get the orbit of
), a discrete form of orbital dynamics. Iterate this process to get the orbit of 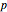 .
.
Contributed by: Gordon Hughes (June 2017)
Open content licensed under CC BY-NC-SA
Snapshots
Details
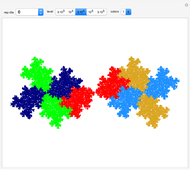
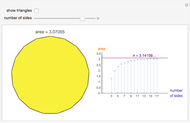
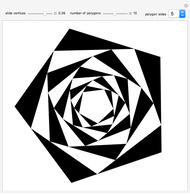
Most orbits are eventually periodic as shown in snapshot 1, but nonperiodic orbits do exist for most regular  -gons. If you are patient, you can find one with the regular pentagon, with
-gons. If you are patient, you can find one with the regular pentagon, with 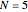 .
.
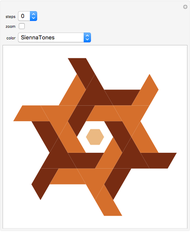
Snapshot 2 shows the beginning of a nonperiodic orbit. In the limit, this orbit produces a fractal image, which can be seen in more detail at [1].
In [2], Jürgen Moser used the landmark KAM theorem, named after A. Kolmogorov, V. Arnold and J. Moser, to show that there is typically a nonzero measure of initial conditions that lead to a stable solar system, but these initial conditions are unknown, and this is still an open question. Since the KAM theorem is very sensitive to continuity, Moser suggested a "toy model" based on orbits around a polygon where continuity would fail. This is now called the outer billiards map.
In [3], Richard Schwartz showed that if the polygon was in a certain class of "kites", orbits could diverge and stability fail. The special case of a regular polygon was settled earlier in 1989 when F. Vivaldi and A. Shaidenko [4] showed that all obits are bounded.
The author of this Demonstration met with Moser at Stanford University in that same year to discuss the canonical structures that always arise in the regular case. Moser suggested that a study of these structures would be an interesting exercise in recreational mathematics. This is exactly what it has become over the past 28 years, but the study of these structures has proven to be a difficult task except for a few simple  -gons such as
-gons such as 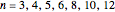 .
.
See [5] for an extensive history of the outer billiards map. The special case of a regular polygon is covered in [6].
References
[1] G. Hughes, "Dynamics of Polygons." (Jun 20, 2017) www.dynamicsofpolygons.org.
[2] J. Moser, "Is the Solar System Stable?” (Jun 20, 2017) abel.math.harvard.edu/archive/118r_spring _ 05/docs/moser.pdf.
[3] R.E. Schwartz, "Unbounded orbits for outer billiards" , Journal of Modern Dynamics 3 (2007)
[4] F. Vivaldi and A. Shaidenko, "Global Stability of a Class of Discontinuous Dual Billiards," Communications in Mathematical Physics, 110(4), 1987 pp. 625–640. doi:10.1007/BF01205552.
[5] G. Hughes, "Chronology of the Outer Billiards Map (Tangent Map)." (Jun 20, 2017) www.dynamicsofpolygons.org/Chronology.
[6] G. Hughes, "Outer Billiards on Regular Polygons." (Jun 20, 2017) arxiv.org/abs/1311.6763.
[7] S. Tabachnikov, Geometry and Billiards, Providence: American Mathematical Society, 2005.
Permanent Citation