PR4 Coding of a Magnetic Hard Drive

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
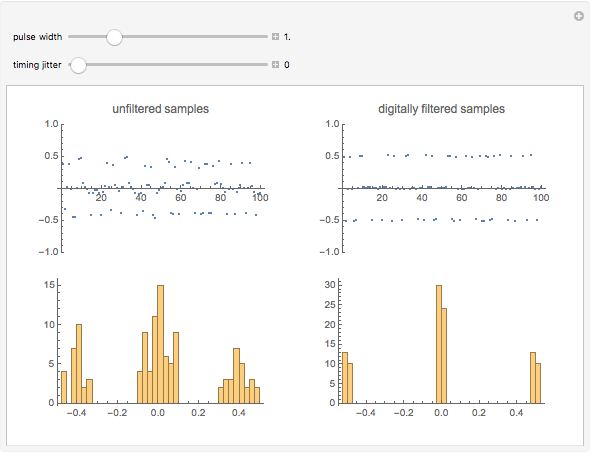
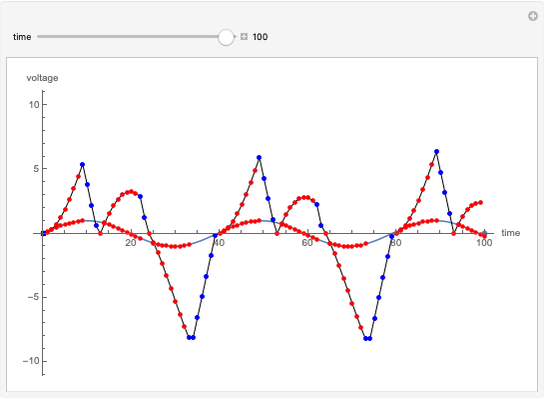
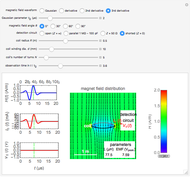
This Demonstration simulates the received signal from a PR4 encoded channel of a magnetic hard disk. PR4 encoding is a type of partial response maximum likelihood (PRML) technique. Unlike the peak detect technique, PRML samples the analog signal received from the disk at times other than the interval of peak response of a magnetic transition. Also, signals from adjacent transitions are allowed to overlap, producing what is known as intersymbol interference (ISI). A digital filter is used to eliminate the effect of ISI.
Contributed by: Charles Masenas (January 2018)
Open content licensed under CC BY-NC-SA
Snapshots
Details
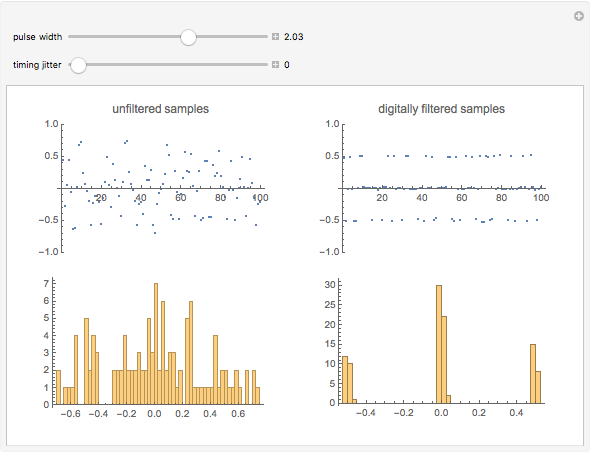
The analog read pulse here is modeled as a Lorentzian function of pulse width measured at half height.
Samples of the recorded data are read as one of three states:  ,
,  or
or 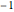 . Samples read as either
. Samples read as either 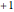 or
or 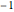 are decoded as 1. Samples of 0 are decoded as 0. This coding makes sense in the context of the magnetic medium. The magnetic medium comprises areas (domains) having polarity dependent on alignment of poles (North and South) within a domain. Transitions between domains produce either a positive polarity (North to South) or negative polarity (South to North) pulse as the read head passes over the transition area. A pulse of one polarity must necessarily be followed by a pulse of the opposite polarity. Thus in writing a 0, no transition is induced in the magnetic medium and no pulse is read from the medium. In writing a 1, a transition is induced and either a positive or negative pulse is read from the medium.
are decoded as 1. Samples of 0 are decoded as 0. This coding makes sense in the context of the magnetic medium. The magnetic medium comprises areas (domains) having polarity dependent on alignment of poles (North and South) within a domain. Transitions between domains produce either a positive polarity (North to South) or negative polarity (South to North) pulse as the read head passes over the transition area. A pulse of one polarity must necessarily be followed by a pulse of the opposite polarity. Thus in writing a 0, no transition is induced in the magnetic medium and no pulse is read from the medium. In writing a 1, a transition is induced and either a positive or negative pulse is read from the medium.
In the technique known as "peak detect," the read signal is sampled at the position of the center of the read pulse and if it exceeds either a positive or negative threshold, a 1 is detected. If the sampled amplitude does not exceed one of the thresholds, a 0 is detected.
In PR4, the read pulse is sampled on the shoulders. One read pulse is sampled twice (this does not require twice the samples of peak detect because the pulses are allowed to overlap). A twice-sampled pulse can be thought of as two adjacent ones (or negative ones). An isolated pulse would give samples 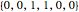 . An isolated pulse of opposite polarity would give samples
. An isolated pulse of opposite polarity would give samples 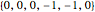 . Adjacent transitions thus yield samples of
. Adjacent transitions thus yield samples of  (i.e. the sampled sum of the adjacent pulses). This explains why reading involves three distinct levels of the read signal. The fact that sampling points of adjacent pulses overlap is referred to as intersymbol interference (ISI). This has the advantages of density and correlation between sampled points. There exists undesirable overlap of the pulses beyond the two desired sampling points per pulse. A digital filter is used to cancel out the undesirable ISI. This Demonstration shows the result of filtering.
(i.e. the sampled sum of the adjacent pulses). This explains why reading involves three distinct levels of the read signal. The fact that sampling points of adjacent pulses overlap is referred to as intersymbol interference (ISI). This has the advantages of density and correlation between sampled points. There exists undesirable overlap of the pulses beyond the two desired sampling points per pulse. A digital filter is used to cancel out the undesirable ISI. This Demonstration shows the result of filtering.
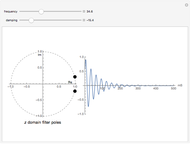
The simulated digital filter is a 17 tap filter. The coefficients are recalculated for every change in pulse width.
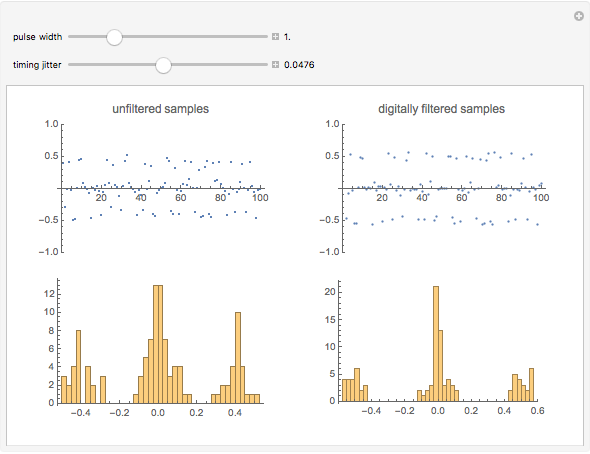
Jitter in the simulation is randomly added to each magnetic transition response, so jitter of adjacent samples is uncorrelated.
This Demonstration shows results of digital filtering of the PR4 read samples to remove ISI. It also shows effects of the width of the read pulse and jitter.
References
[1] "Computer Peripherals." School of Computer Engineering, Nanyang Technological University, Singapore. (Dec 20, 2017) www.lintech.org/comp-per/09PRML.pdf.
[2] Wikipedia. "Partial-Response Maximum-Likelihood." (Dec 20, 2017) en.wikipedia.org/wiki/Partial-response_maximum-likelihood.
[3] The PC Guide. "Partial Response, Maximum Likelihood (PRML)." (Dec 20, 2017) www.pcguide.com/ref/hdd/geom/dataPRML-c.html.
[4] Forensics Wiki. "PRML Read Channels: Bringing Higher Densities and Performance to New-Generation Hard Drives." (Dec 20, 2017) forensicswiki.org/w/images/c/c6/Maxtor_PRML_Read _Channels.pdf.
Permanent Citation