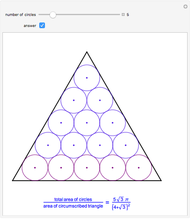
Packing a Circle with Circles

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
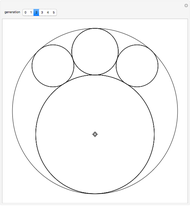
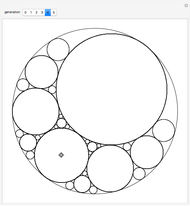
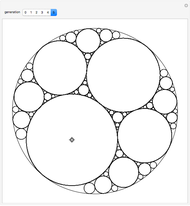
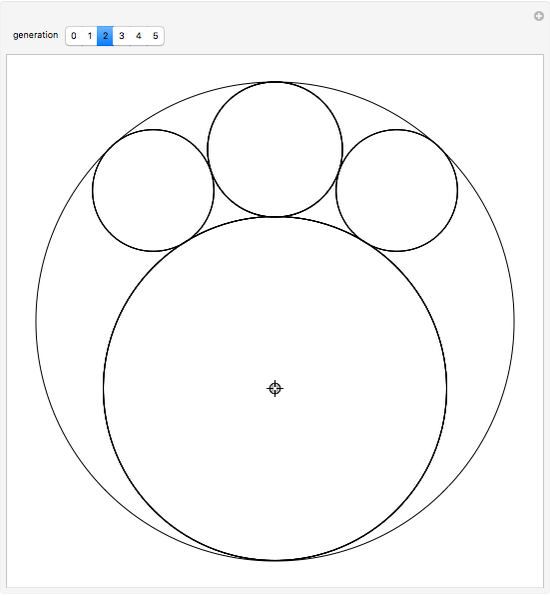
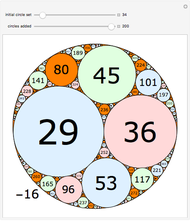
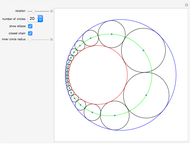
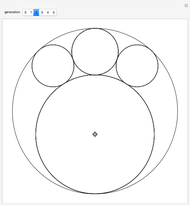
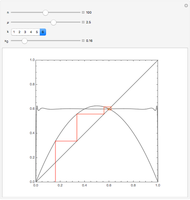
Two circles with a radius initially set to  are placed in the unit circle. When you drag the locator, the centers and radii of the circles change. The rule for the iteration is to construct the largest possible circles in the curvilinear triangles.
are placed in the unit circle. When you drag the locator, the centers and radii of the circles change. The rule for the iteration is to construct the largest possible circles in the curvilinear triangles.
Contributed by: Hans-Joachim Domke (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
The packing shown in this Demonstration is similar to that in "The Circles of Descartes" Demonstration, but uses a different mathematical approach than the Descartes circle theorem to find the solution of the inscribed circle 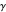 of three mutually tangent circles.
of three mutually tangent circles.
Let the inscribed circle 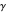 meet the three given circles at
meet the three given circles at 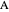 ,
,  , and
, and 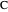 . Then the equation
. Then the equation  reflects the fact that the point
reflects the fact that the point  lies on the circle with center
lies on the circle with center  and radius
and radius  . For
. For 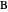 and
and 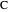 the equations are similar and for
the equations are similar and for 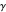 the equation is
the equation is 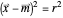 . Because
. Because 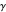 is tangent to one of the three circles at
is tangent to one of the three circles at 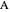 ,
, 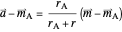 and hence
and hence 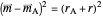 .
.
The coordinates of 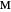 and the value for
and the value for  are three unknowns, but there are three equations, so the solutions are well determined. There are two solutions because the equations are quadratic but not all of them are valid.
are three unknowns, but there are three equations, so the solutions are well determined. There are two solutions because the equations are quadratic but not all of them are valid.
For the solution circles that are tangent to the unit circle, one of the equations reduces to 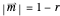 .
.
Permanent Citation