Wolfram Demonstrations Project

12,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

Pál Joints

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

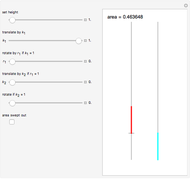
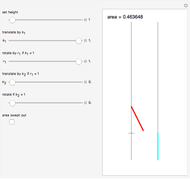
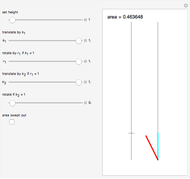
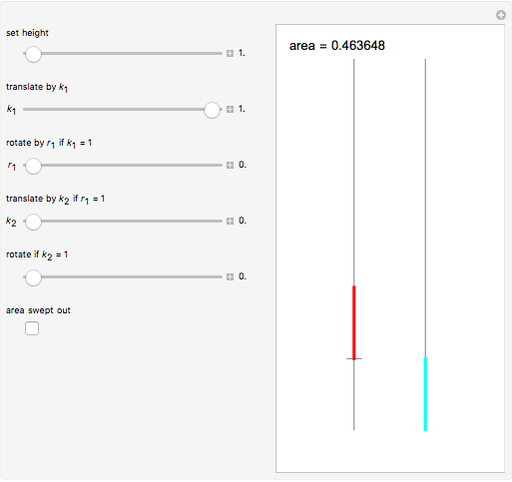
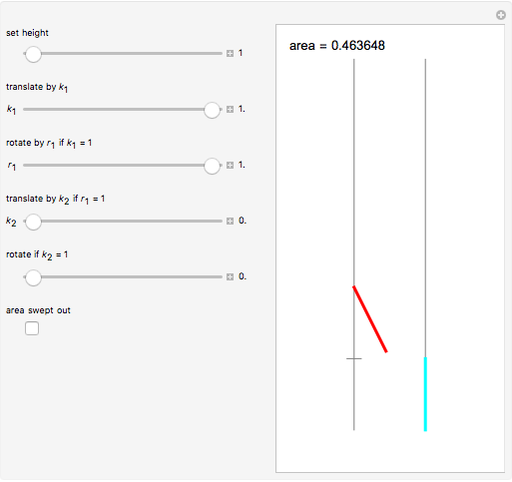
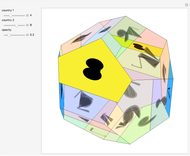
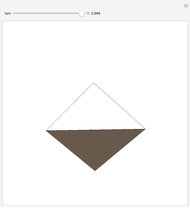
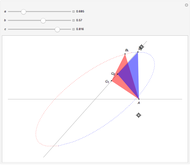
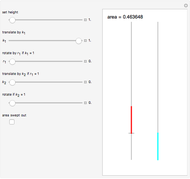
This Demonstration shows a method called Pál joints that lets you move a segment to a parallel segment through an area approaching 0. If the height is , then the area swept out by the segment is 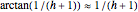. Therefore, given two parallel lines, a unit line segment can be moved continuously from one to the other sweeping out a set of arbitrarily small measure.

Contributed by: Izidor Hafner and Borut Jurcic Zlobec (June 2016)
Open content licensed under CC BY-NC-SA

Snapshots

Details

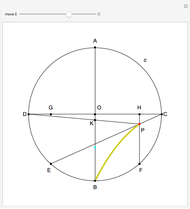
This construction allows the continuous motion of a unit segment back to itself but rotated by 180°, again in a set of arbitrarily small measure [1].

References

[1] Wikipedia. "Kakeya Set. (Jun 9, 2016) en.wikipedia.org/wiki/Kakeya_set.

[2] K. J. Falconer, The Geometry of Fractal Sets, Cambridge, England: Cambridge University Press, 1990.

[3] D. Wells, The Penguin Dictionary of Curious and Interesting Geometry, London: Penguin, pp. 128–129, 1991.

[4] C. Fefferman. Kakeya Needle Problem [Video]. (Jun 9, 2016) www.youtube.com/watch?v=j-dce6QmVAQ.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send