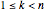Parameterized Families of Elliptic Curves with Large Rational Torsion Subgroups

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
The set of rational points 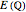 on an elliptic curve
on an elliptic curve 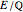 defined over the rationals
defined over the rationals  with at least one rational point
with at least one rational point  is endowed with a group law that can be described geometrically using the chord-and-tangent method. Further, it is a well-known result that if
is endowed with a group law that can be described geometrically using the chord-and-tangent method. Further, it is a well-known result that if 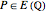 is a rational point of order
is a rational point of order  for
for 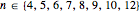 , then
, then 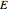 is birationally equivalent to an elliptic curve with an equation
is birationally equivalent to an elliptic curve with an equation 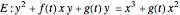 , where
, where 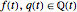 and
and 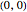 is a rational point of order
is a rational point of order  . That is, all elliptic curves
. That is, all elliptic curves 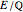 with a rational point of order
with a rational point of order  are in a one-parameter family if
are in a one-parameter family if 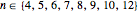 .
.
Contributed by: Christopher Grattoni (June 2015)
Open content licensed under CC BY-NC-SA
Snapshots
Details
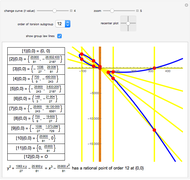
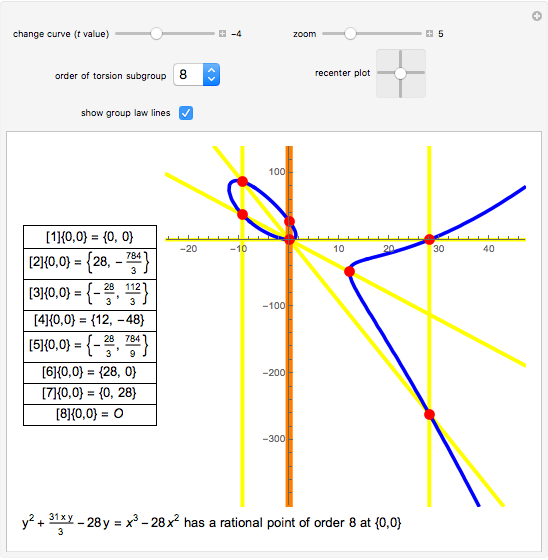
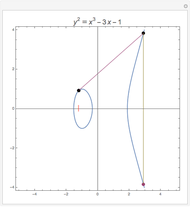
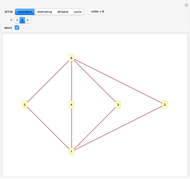
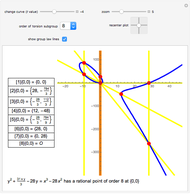
Snapshot 1: this elliptic curve has a rational point of order 8, and a geometric representation of the group law is visible
Snapshot 2: this elliptic curve has a rational point of order 5
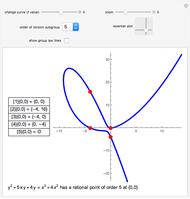
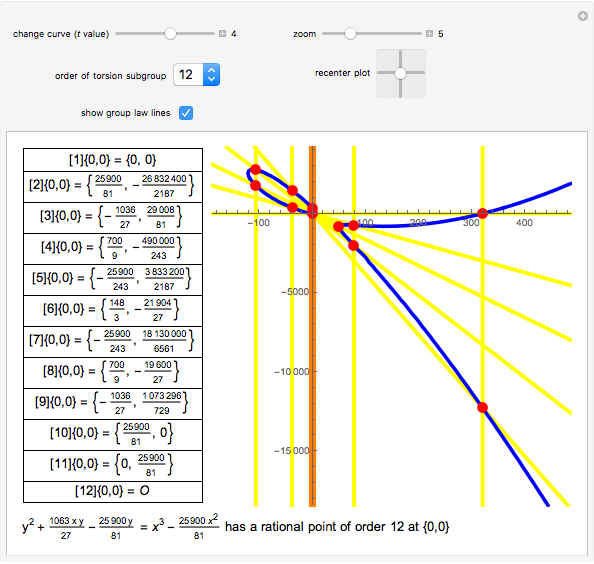
Snapshot 3: this elliptic curve has a rational point of order 12, and a geometric representation of the group law is visible
The notation 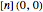 for an elliptic curve
for an elliptic curve  is the multiplication-by-
is the multiplication-by- map on
map on 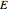 . That is, if we call the group law on the elliptic curve "addition," then
. That is, if we call the group law on the elliptic curve "addition," then 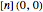 is defined as "adding"
is defined as "adding" 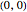 to itself
to itself  times. The identity element for this group law is the point at infinity
times. The identity element for this group law is the point at infinity 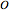 for the projective plane. Two points sum to
for the projective plane. Two points sum to 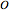 when they intersect the same vertical line. The yellow lines in the Demonstration are the lines that arise from repeatedly adding
when they intersect the same vertical line. The yellow lines in the Demonstration are the lines that arise from repeatedly adding 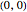 to itself. The vertical orange line is meant to signify the final sum,
to itself. The vertical orange line is meant to signify the final sum, 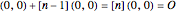 . The Demonstration "Addition of Points on an Elliptic Curve over the Reals" shows this chord-and-tangent formulation of the elliptic curve group law.
. The Demonstration "Addition of Points on an Elliptic Curve over the Reals" shows this chord-and-tangent formulation of the elliptic curve group law.
You may want to know how to compute 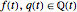 such that
such that 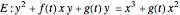 has a rational point of order
has a rational point of order 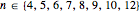 at the point
at the point  . First, suppose
. First, suppose  has a rational point of order
has a rational point of order  . This implies that
. This implies that 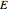 is birationally equivalent to an elliptic curve in Tate normal form,
is birationally equivalent to an elliptic curve in Tate normal form,  for
for  , such that
, such that  is a rational point of order
is a rational point of order  . Next, compute
. Next, compute 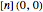 and suppose it equals
and suppose it equals 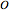 . This allows one to find a relation between
. This allows one to find a relation between  and
and 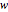 . Once this relation is found, use this in
. Once this relation is found, use this in 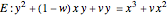 , which results in the desired one-parameter family of curves with a rational point of order
, which results in the desired one-parameter family of curves with a rational point of order  for
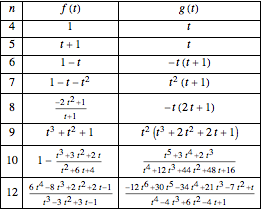
for 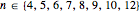 . These results are summarized below:
. These results are summarized below:
References
[1] J. H. Silverman, The Arithmetic of Elliptic Curves, New York: Springer-Verlag, 1986.
[2] I. García, M. A. Olalla, and J. M. Tornero, "Computing the Rational Torsion of an Elliptic Curve Using Tate Normal Form," Journal of Number Theory, 96(1), 2002 pp. 76–88. doi:10.1006/jnth.2002.2780.
[3] E. V. Flynn and C. Grattoni, "Descent via Isogeny on Elliptic Curves with Large Rational Torsion Subgroups," Journal of Symbolic Computation, 43(4), 2008 pp. 293–303. doi:10.1016/j.jsc.2007.11.001.
Permanent Citation