Wolfram Demonstrations Project

12,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

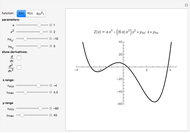
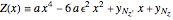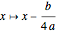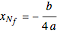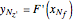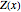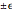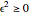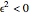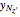Parameters for Plotting a Quartic

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

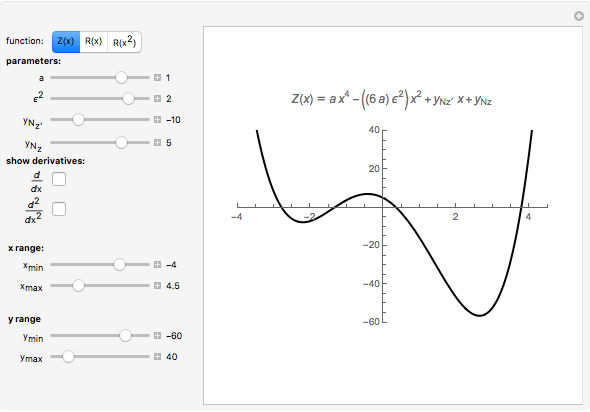
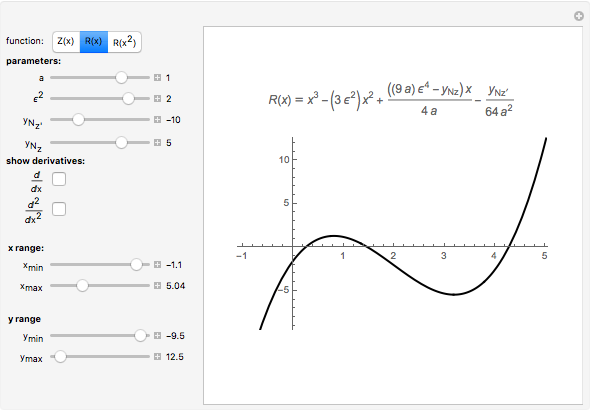
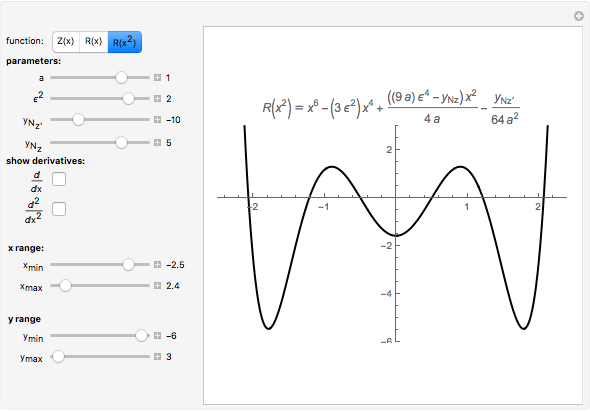
The general quartic 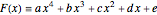can be brought into the reduced form

[more]

by means of the translation . If , then and .

The coordinates of the two points of inflection of are , where .

When , there are two real points of inflection and hence three real turning points. When , both points of inflection are complex and hence there is only one real turning point.

Since , , and are directly related to the geometry of the quartic, this Demonstration offers a more intuitive insight regarding how the shape of the curve is related to the coefficients of the reduced form .

[less]

Contributed by: Thomas Mueller and R.W.D. Nickalls (March 2011)
Open content licensed under CC BY-NC-SA

Snapshots

Details

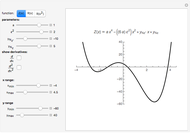
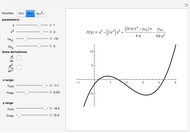
The four roots of the reduced quartic equation can be expressed in terms of just three parameters, say 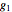, , 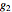, 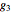where 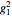, , 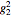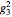are the roots of the resolvent cubic equation 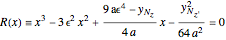, known as Euler's cubic. Note that are the six roots of the resolvent sextic 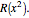Thus, the key to solving the quartic is to first solve the resolvent cubic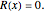

For a more detailed discussion see R. W. D. Nickalls, "The Quartic Equation: Invariants and Euler's Solution Revealed," The Mathematical Gazette, 94, 2009 pp. 66–75.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send