Wolfram Demonstrations Project

12,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

Particle in an Infinite Circular Well

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

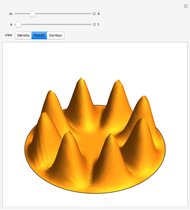
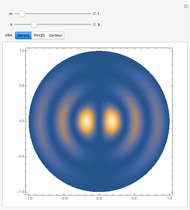
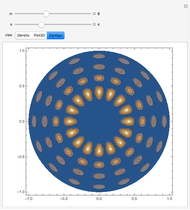
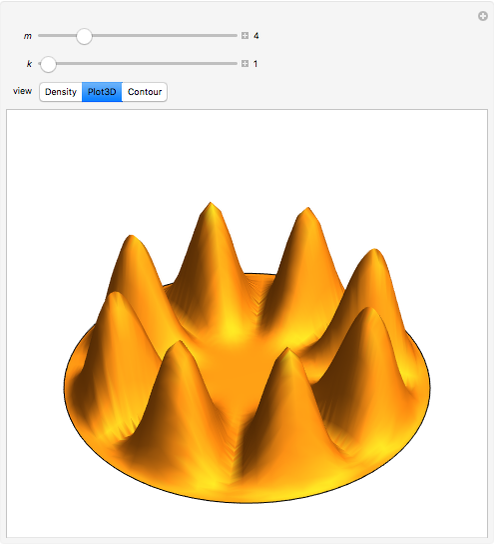
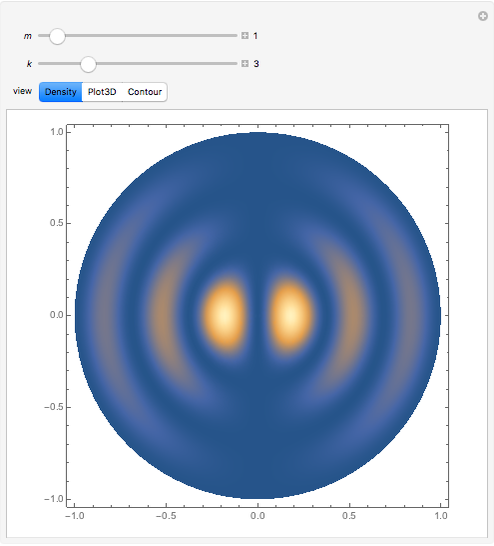
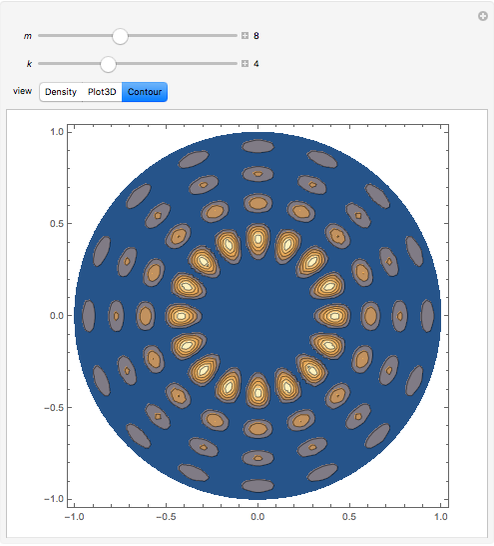
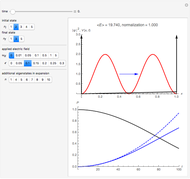
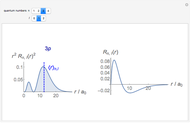
This Demonstration solves the quantum-mechanical problem of a particle confined to a disk, which can be called an infinite 2D circular well. The probability densities for several energy eigenstates are plotted. The azimuthal quantum number 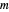, equal to the number of angular nodes, determines the angular momentum . The radially excited state energies depend on the zeros of the Bessel function .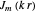

Contributed by: Enrique Zeleny (August 2013)
Based on a program by: Michael Trott
Open content licensed under CC BY-NC-SA

Snapshots

Details

The solutions are of the form 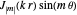and 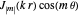with the quantized energy levels

,

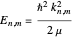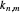where is the Planck constant, is the mass and is the zero of the Besssel function .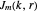

References

[1] R. W. Robinett, "Visualizing the Solutions for the Circular Infinite Well in Quantum and Classical Mechanics," American Journal of Physics, 64(4), \:200e1996 pp. 440–446.

[2] R. W. Robinett, Quantum Mechanics, Classical Results, Modern Systems and Visualized Examples, 2nd ed., Oxford: Oxford University Press, 2006.

[3] R. W. Robinett, "Quantum Mechanics of the Two-Dimensional Circular Billiard Plus Baffle System and Half-Integral Angular Momentum." arxiv.org/pdf/quant-ph/0307035.pdf.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send