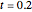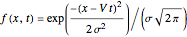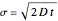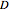Particle Position Distribution Using a Brownian Dynamic Simulation

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
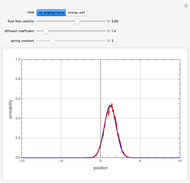
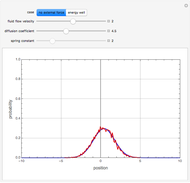
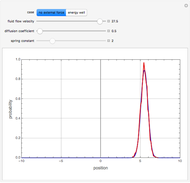
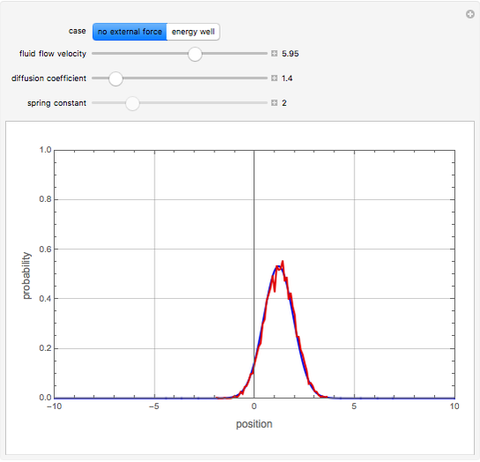
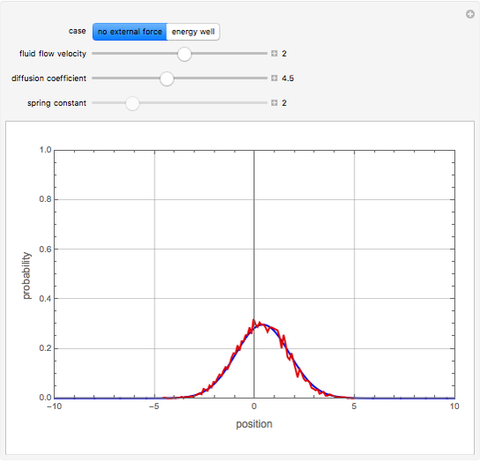
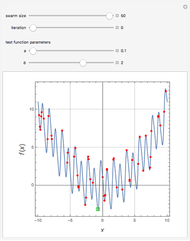
The Brownian dynamics (BD) method is used to solve two case studies for the position distribution of a particle in: (1) a flowing fluid under no external force and Brownian diffusion; and (2) a quadratic energy well with Brownian diffusion. For both cases, the explicit Euler stochastic differential equation (SDE) method is employed [1].
[more]
Contributed by: Housam Binous and Brian G. Higgins (November 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Reference
[1] K. J. Beers, Numerical Methods for Chemical Engineering, Cambridge: Cambridge University Press, 2007.
Permanent Citation