Pascal's Mystic Hexagon

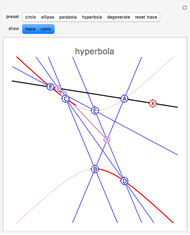
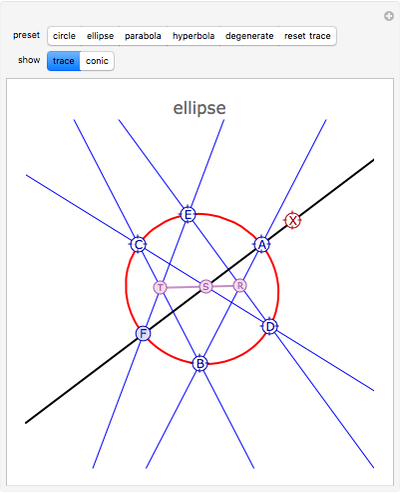
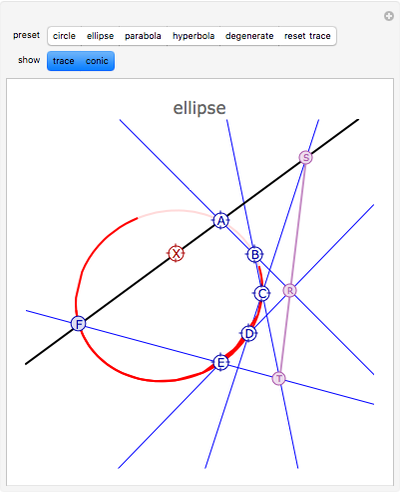
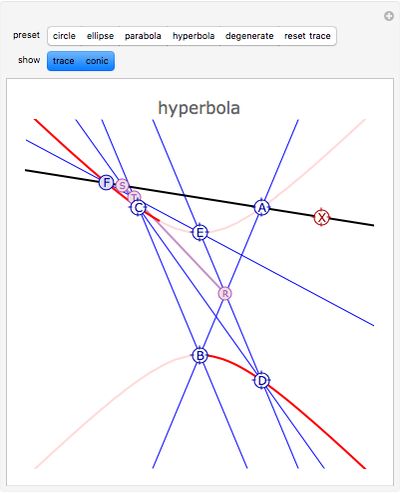
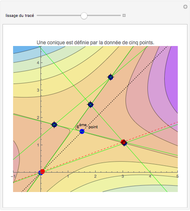
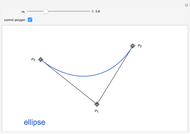
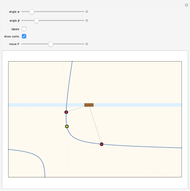
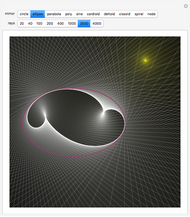
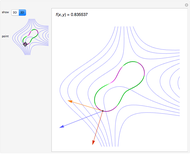
Pascal discovered that if hexagon ABCDEF is inscribed in a conic section, the points of intersection RST of the pairs of opposite chords are collinear. You can generate the conic through points A, B, C, D, E, since F can be derived from an arbitrary line AX through A. Moving X and F traces the conic. Move A, B, C, D, or E to get a new conic that passes through them.

Contributed by: Michael Rogers (Oxford College/Emory University)

Show Initialization Code

(56 lines omitted)

Pascal (1640) discovered that if a hexagon (or hexagram) ABCDEF is inscribed in a conic section, then taking opposite chords, the points of intersection R = AB.ED, S = AF.CD, and T = EF.CB are collinear. (If you put the points in the order AECDBF, as in snapshot 2, then the chords are pairs of opposite sides.) Pascal stated his result slightly differently. In effect, his theorem asserts that AF, CD, and RT run through the same point (S). Braikenridge and Maclaurin (1733) discovered how to generate the conic through A, B, C, D, E. The point F can be derived from an arbitrary line AX through A from the following intersections:
R = AB.ED,
S = AX.CD,
T = RS.CB,
F = AX.ET.
Moving X and F traces the conic. You can choose whether just to trace the conic, have the whole conic displayed, or both.

Pascal's "Essai pour les coniques," written in 1640 when he was sixteen, from D. E. Smith, A Source Book in Mathematics, London: Dover, 1959 pp. 326-330.

H. S. M. Coxeter, Introduction to Geometry, 2nd ed., Wiley, 1989.