Path Integrals on Causal Sets


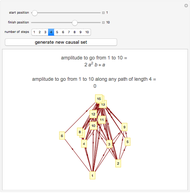
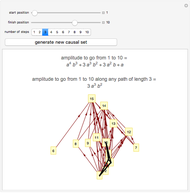
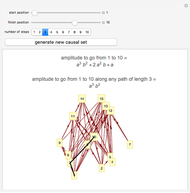
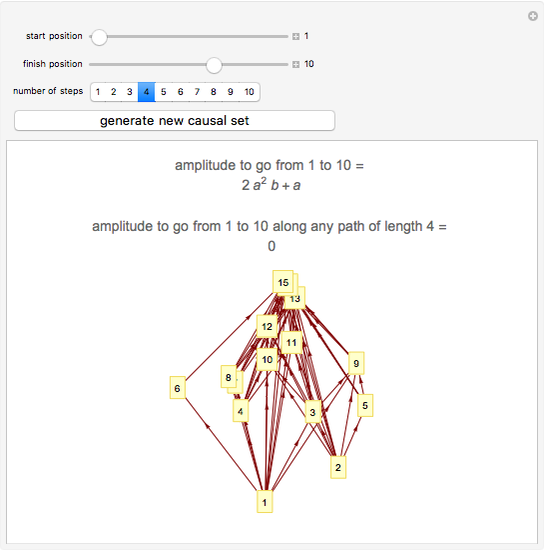
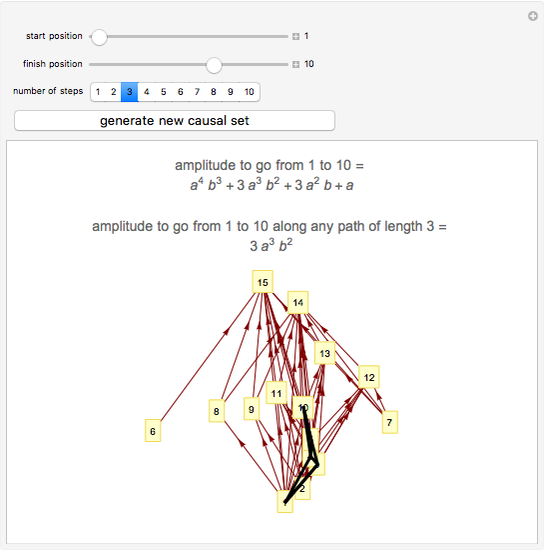
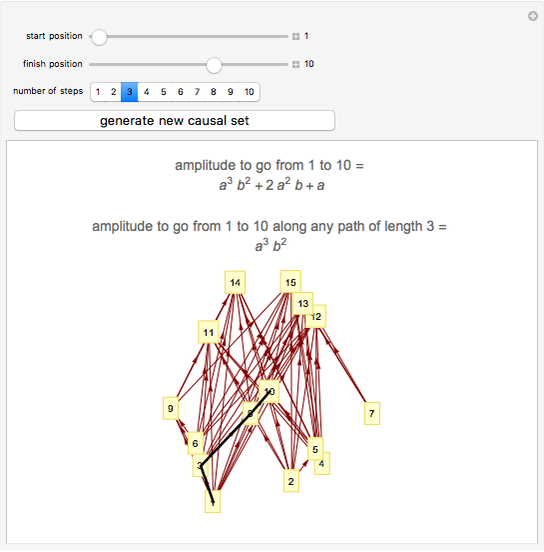
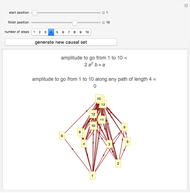
	This shows a randomly generated causal set. The "start position" and "finish position" denote spacetime locations within the causal set. Specifying the "number of steps" then draws all trajectories within the causal set from the start to the specified final step. To perform a quantum mechanical path integral each trajectory of length is assigned an amplitude (a complex number) 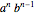. Summing these amplitudes for all trajectories from the start to the finish gives the total amplitude for a particle to travel from the start to the finish.


	Contributed by: Steven Johnston
	Show Initialization Code

Causal set theory is an approach to quantum gravity in which spacetime is discrete. A causal set is a locally finite, partially ordered set. Locations in spacetime are represented by elements of the set and the causal relationships between pairs of locations are represented by the partial order relation. Here the causal set is represented as a directed graph in which the elements of the set are vertices and the relations are directed edges joining related pairs of elements.

A propagator in quantum mechanics is a function of two spacetime locations and can be interpreted as the quantum mechanical amplitude for a particle to travel from one location to the other. It can be obtained by a path integral in which complex numbers are assigned to different trajectories leading from one location to the other. Summing these numbers over all trajectories gives the value of the propagator. In the discrete spacetime of a causal set this sum can be performed explicitly since there are only finitely many trajectories leading from one element to another.

This Demonstration is based on S. Johnston, "Particle Propagators on Discrete Spacetime," Class. Quantum Grav., 25 202001 (arXiv:0806.3083).